Visual representation of the roots of unity
The property that if is a -th root of unity, then and are additive inverses may seem a little abstract — this chapter introduces a visual that makes this concept easier to remember.
Recall that the -th roots of unity are generated by taking the primitive -th root of unity and raising it to successive powers. For example, if , we compute the 4-th roots of unity as
If we were to keep going, the exponents would wrap around modulo 4:
- (by definition of being a 4-th root of unity)
and so on.
Note that the exponent “wraps around” at each multiple of four. Thus, for any and , . Since in our example, we have that
Now recall that addition modulo can be represented as a “clock.” Here, our clock consists of the “hour markers” 0, 1, 2, 3, which are the exponents of
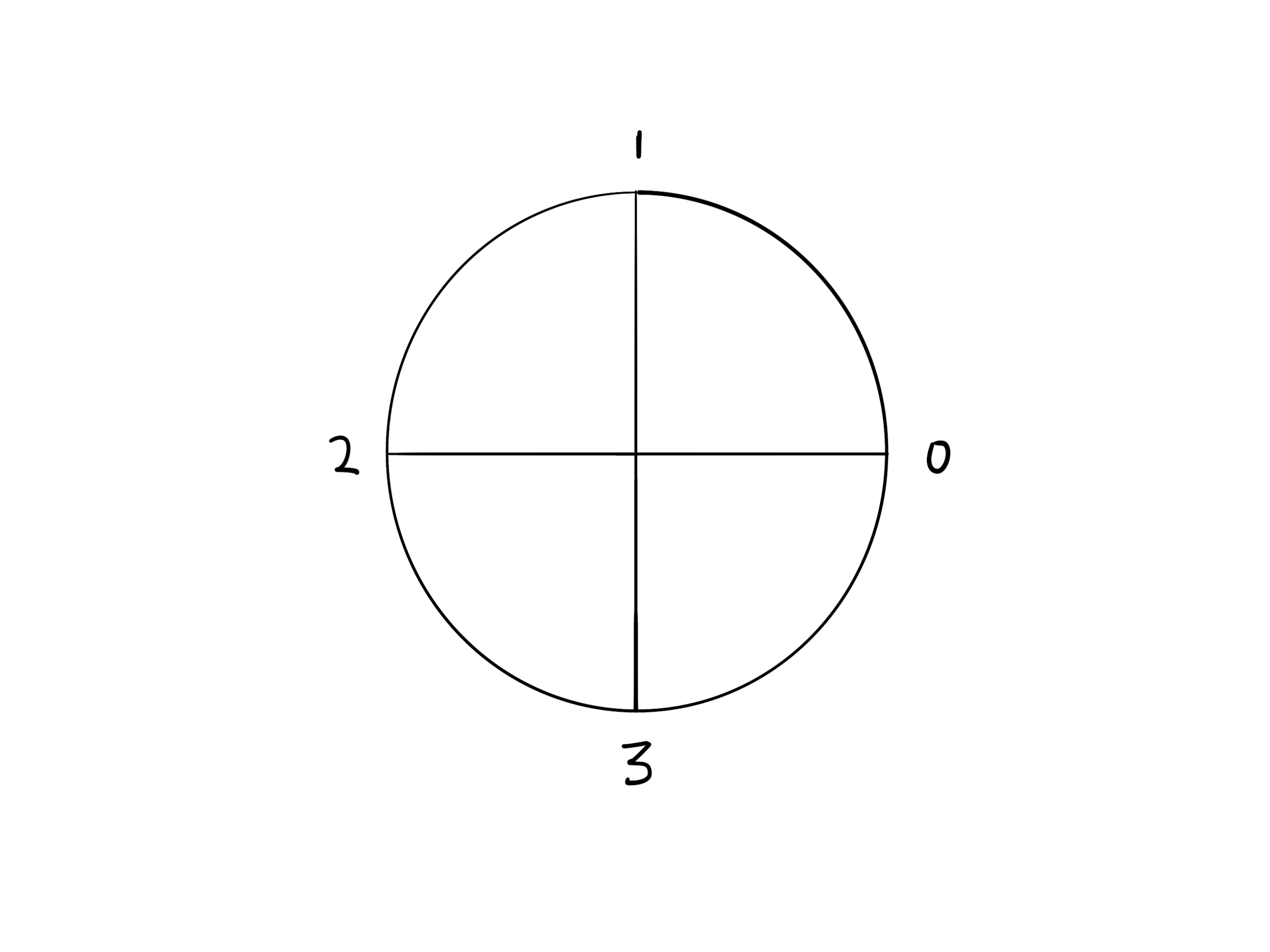
One way to think about this is
“adding two numbers and on the clock is equivalent to multiplying the roots of unity that have exponents and i.e. and .”
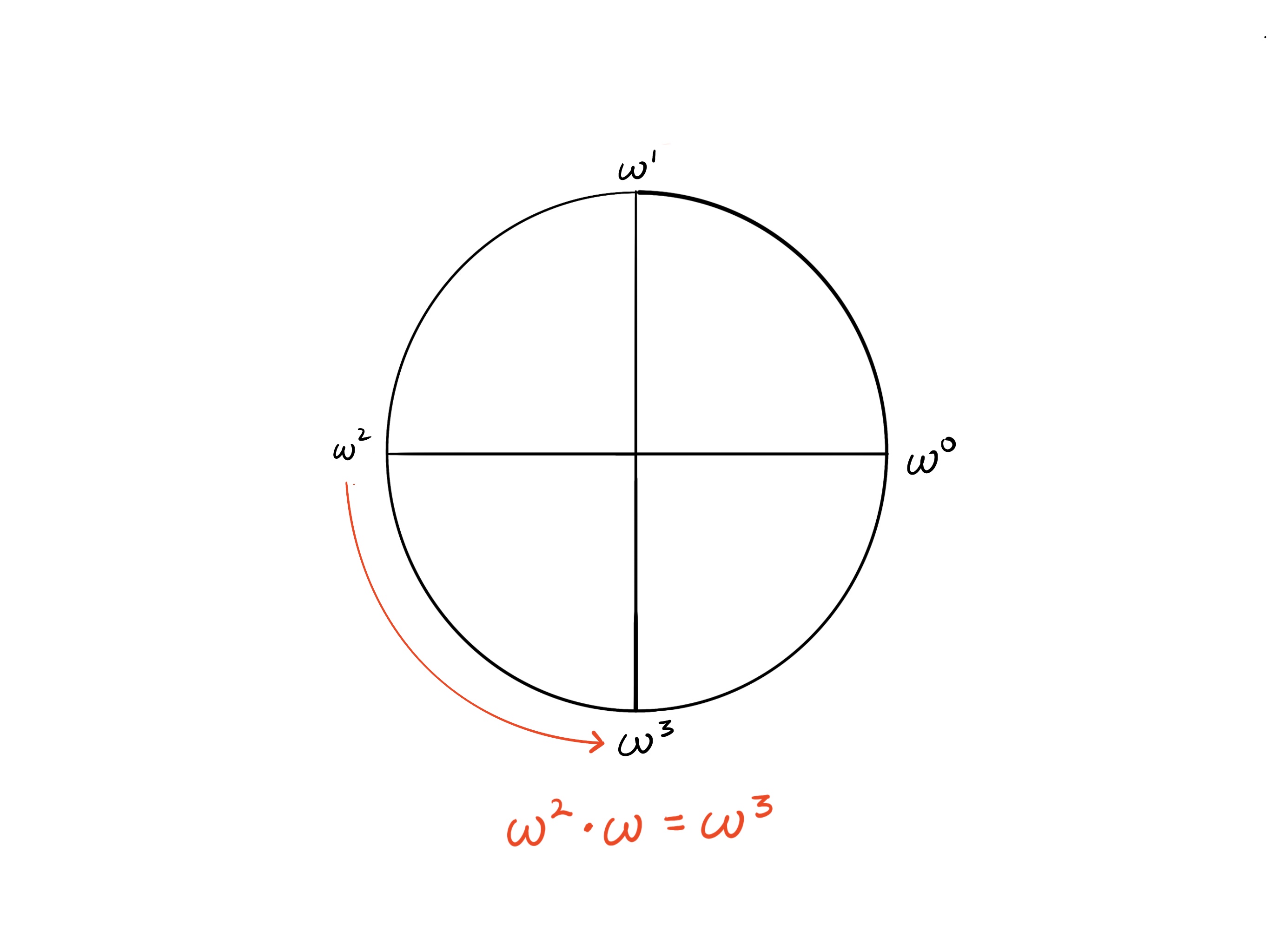
If we take any root of unity and add 1 to the exponent, this is equivalent to multiplying that root of unity by (or just ). For example, multiplying by is the same as adding one to the exponent to get .
Therefore, multiplying a -th root of unity by or adding 1 to the exponent is the same as taking -th step around the circle.
For example, if we multiply by we get , which equals moving forward 1/4-th step:
We can think of generating the roots of unity by starting with and repeatedly adding 1 to the exponent to produce , and so on until we reach at which point the results will wrap around modulo . This is exactly the same as taking steps around the circle.
Visualizing congruences with the unit circle
Let’s expand this circle to include more congruences.
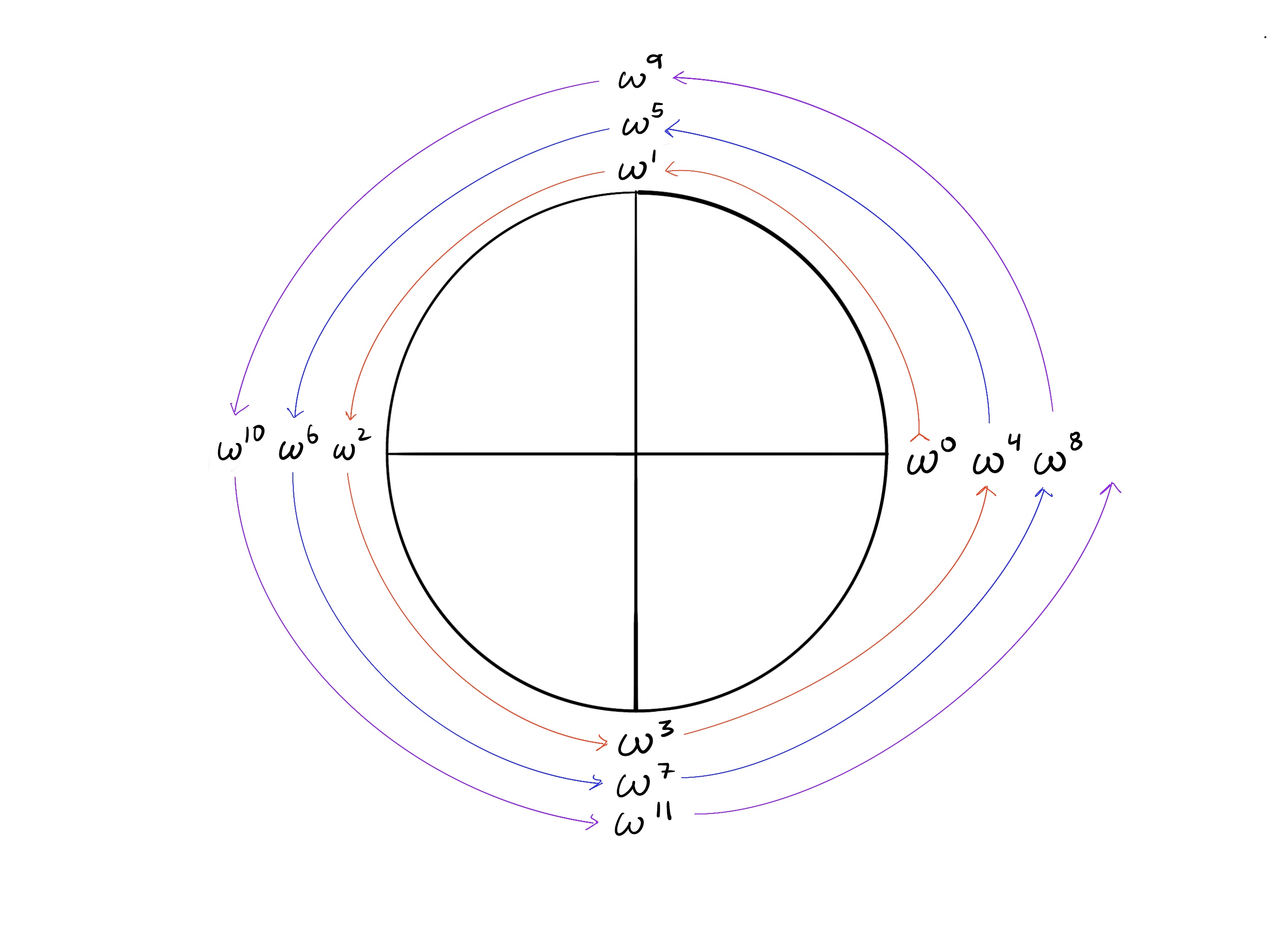
If we multiply and , we will get , which is congruent to , exactly as the chart suggests:
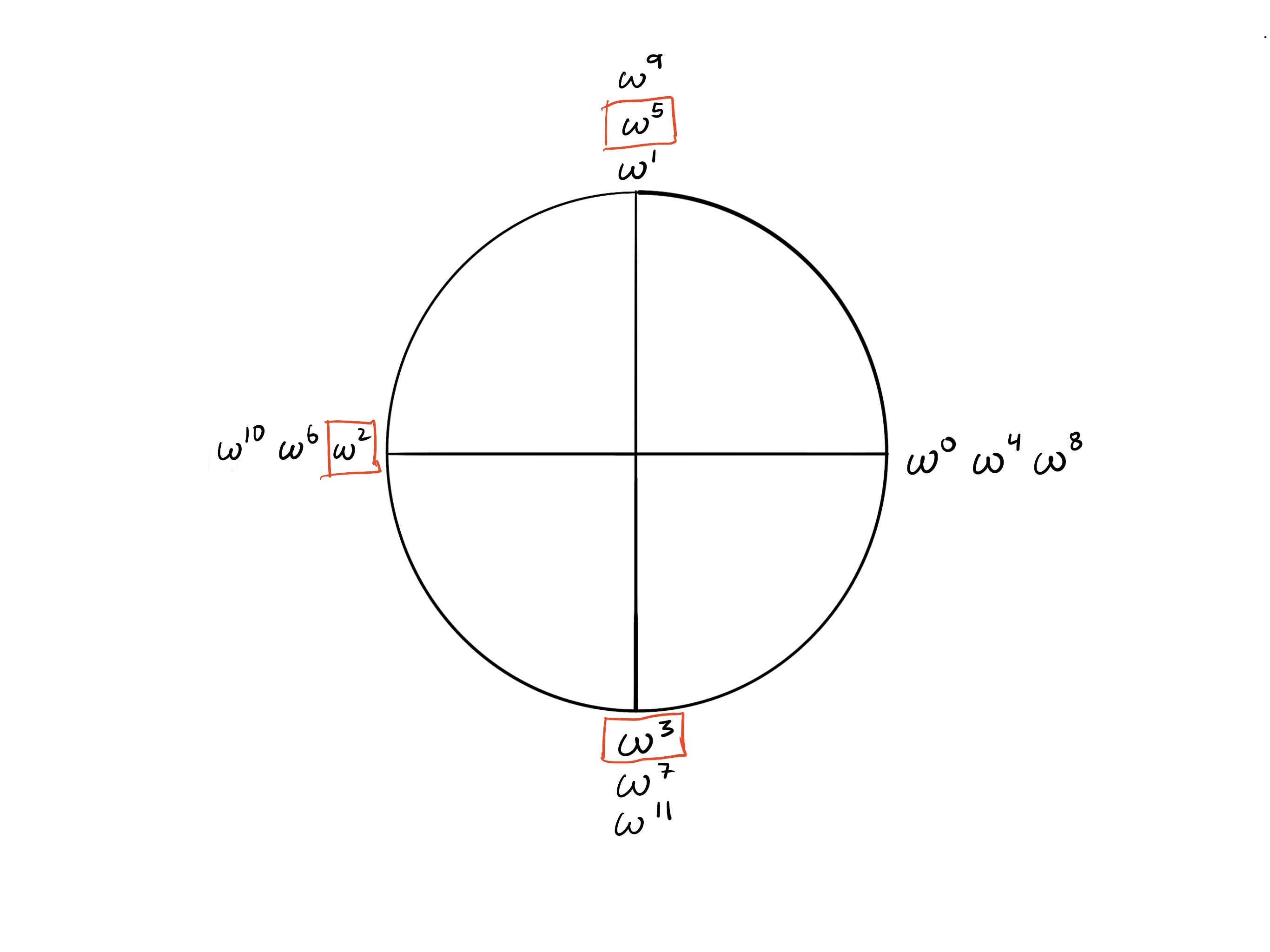
Another way to think about this is starting at and taking 3 steps forward:
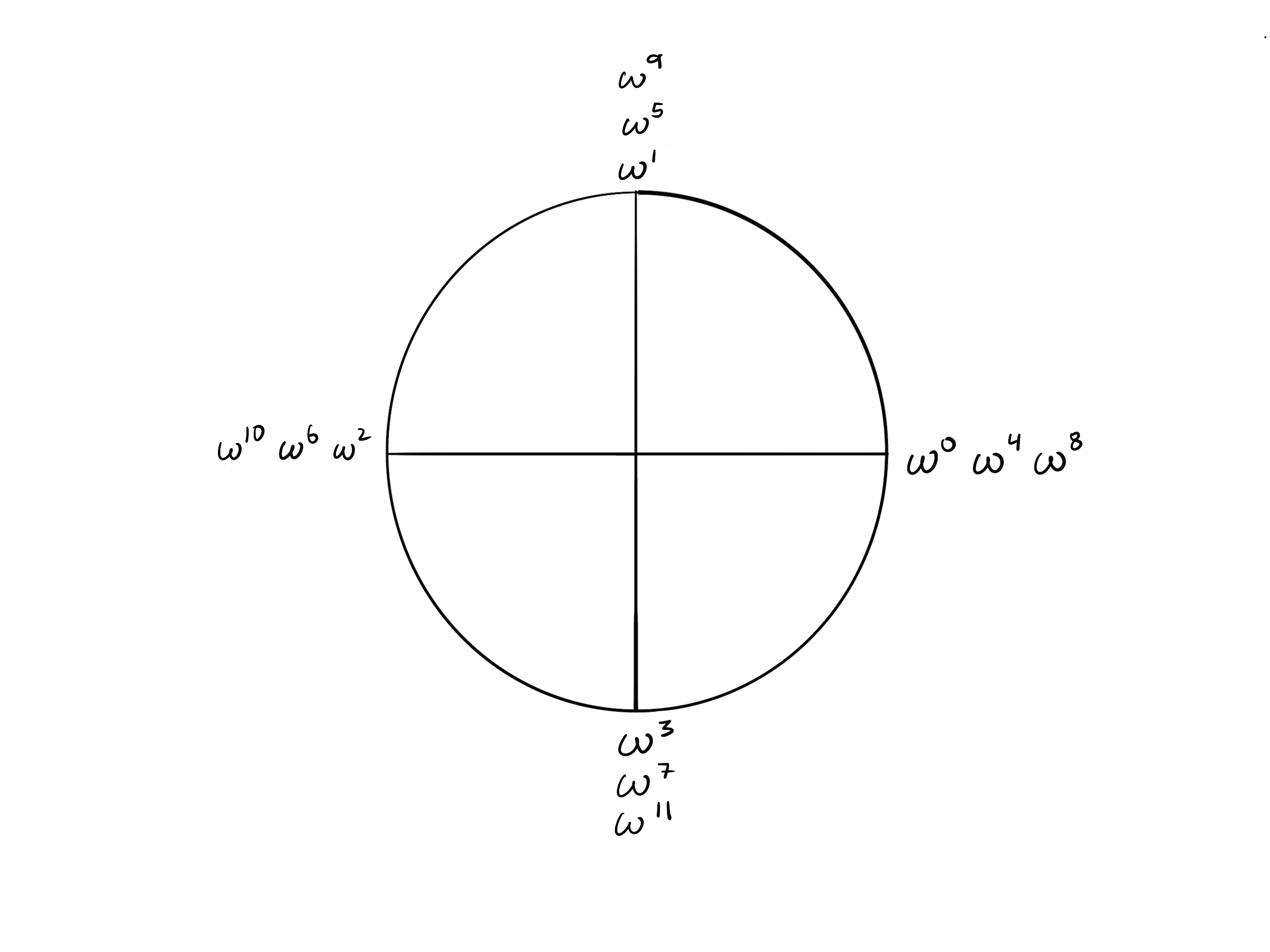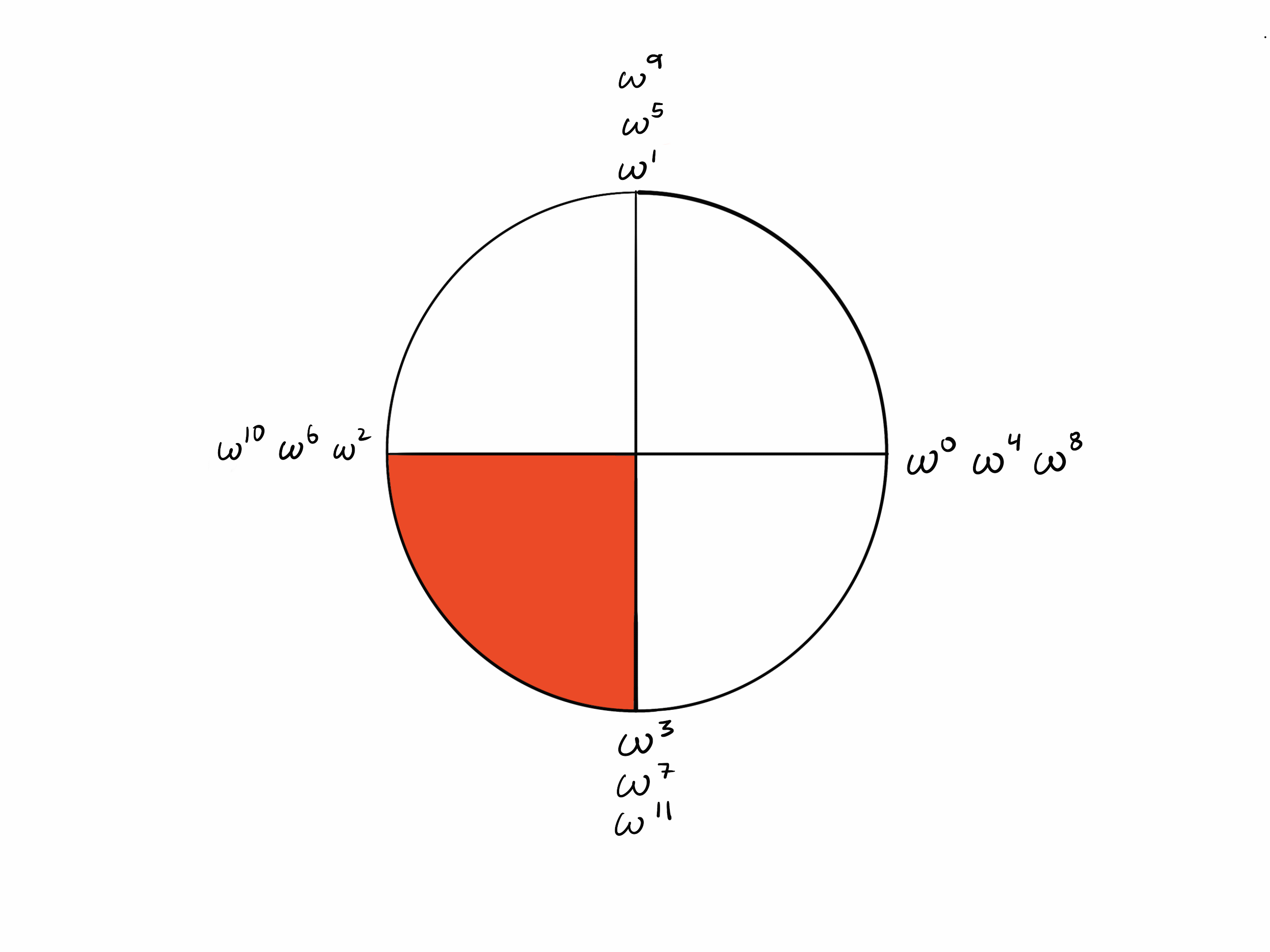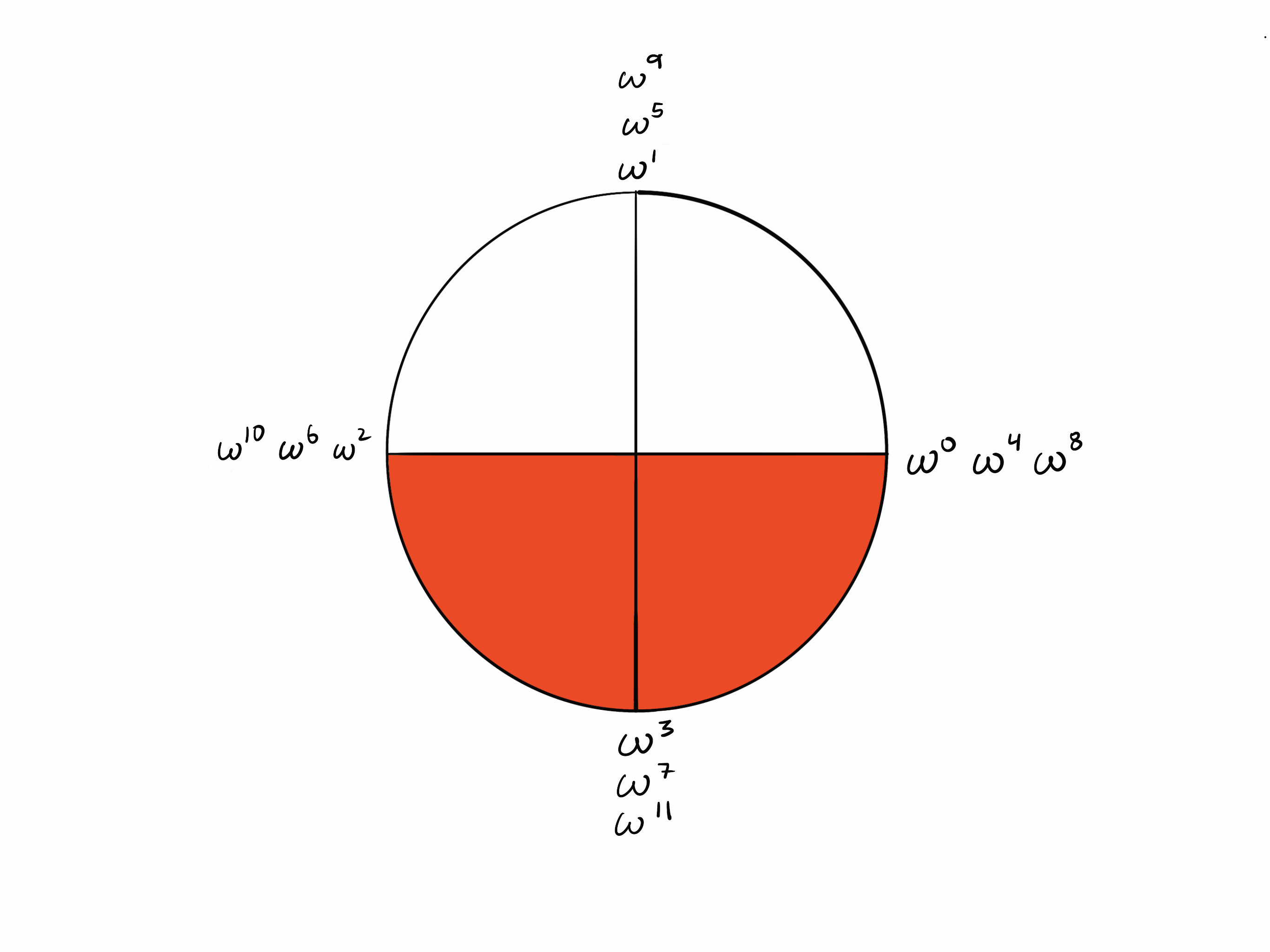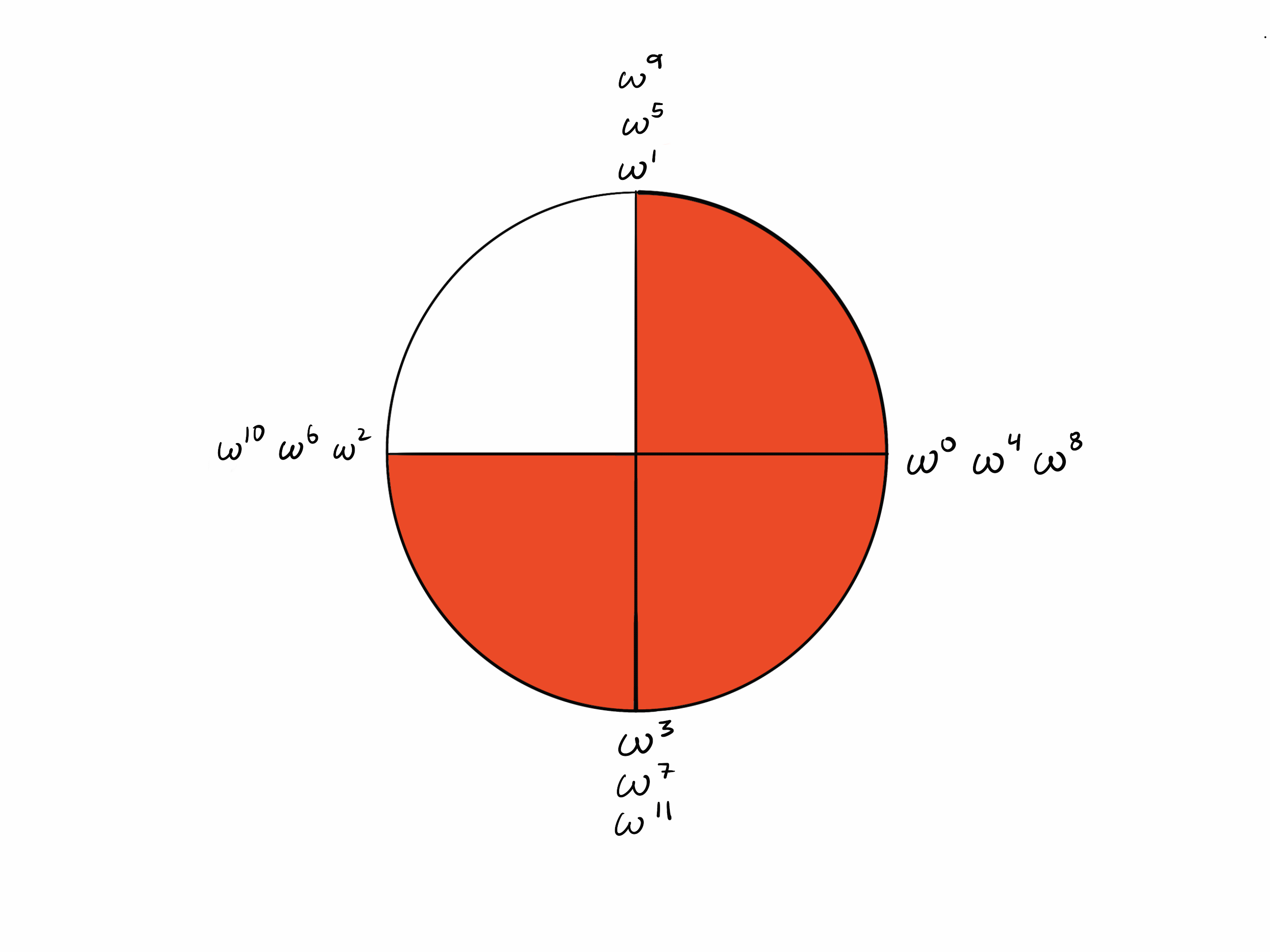
Points k/2 steps apart
Since it takes steps to “walk around” the circle, steps takes you from a point to the opposite point.
Now observe in the circle of that opposite points are additive inverses of each other (they sum to zero). Recall that . Since k = 4,
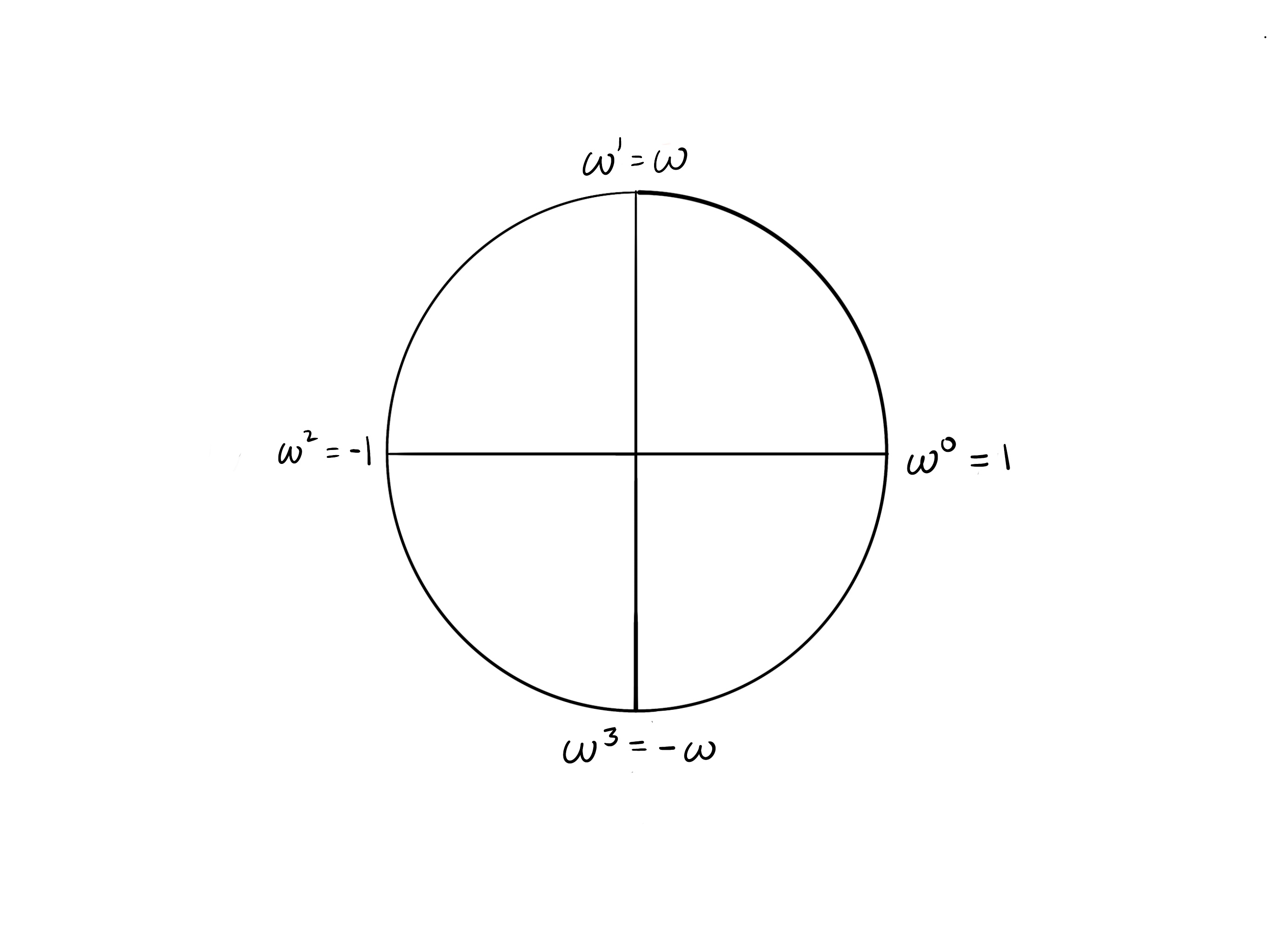
In the example, we have that
Note that we are now adding the roots of unity together, not multiplying them, so the addition of exponents rule does not apply! Don’t confuse with ! Roots of unity are finite field elements, and fields have 2 operations: addition and multiplication.
Examples with other values of k
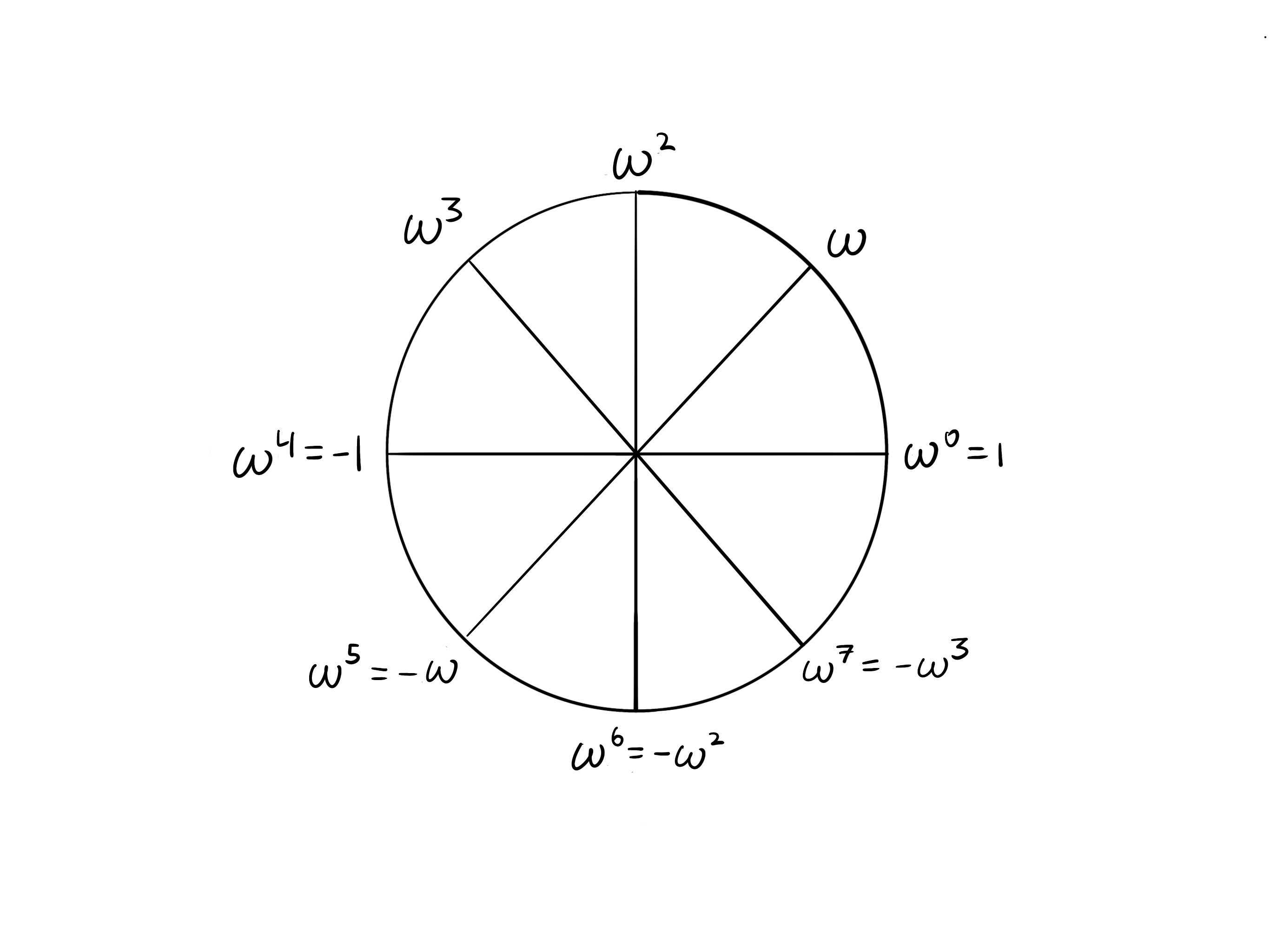
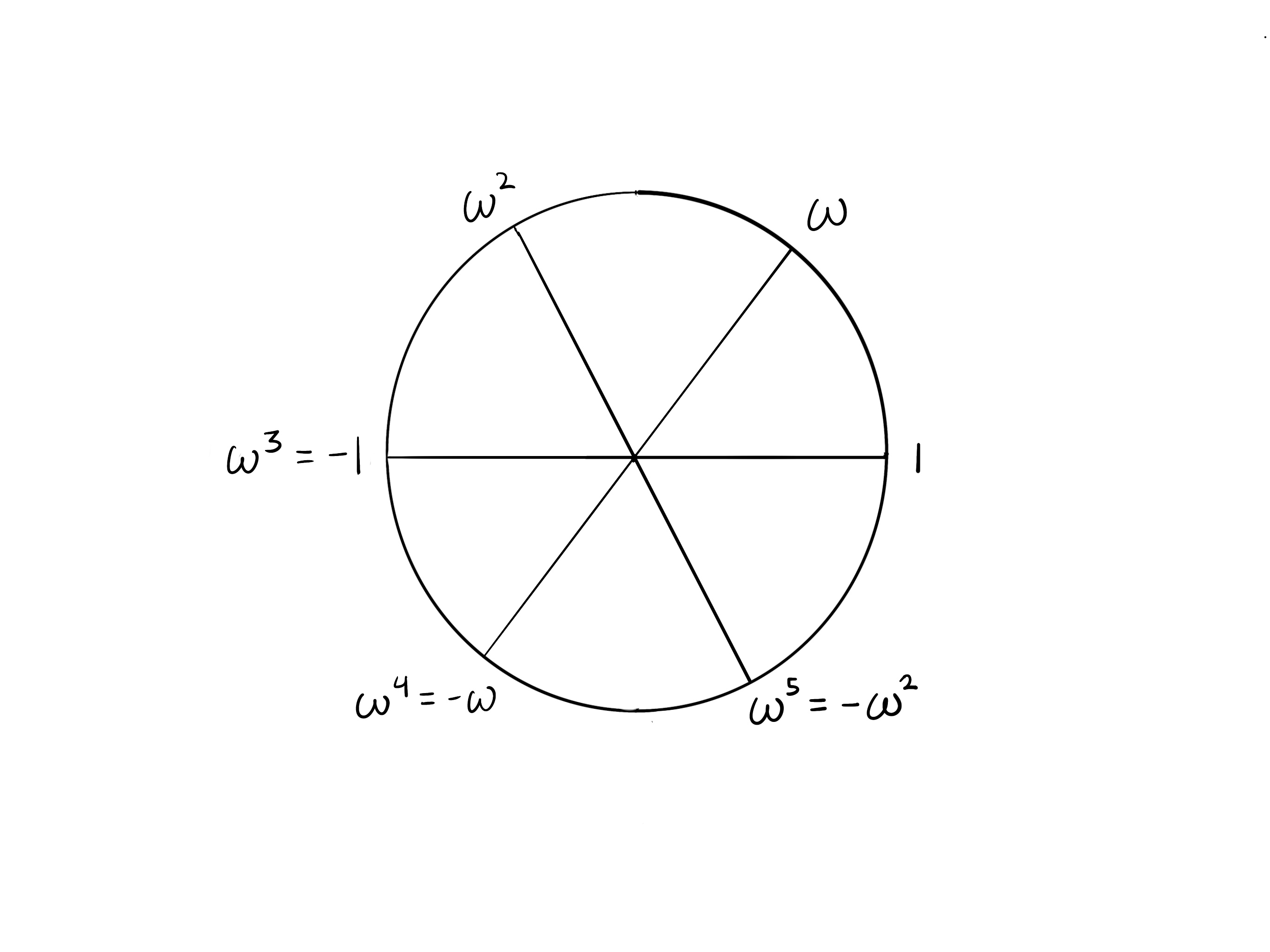
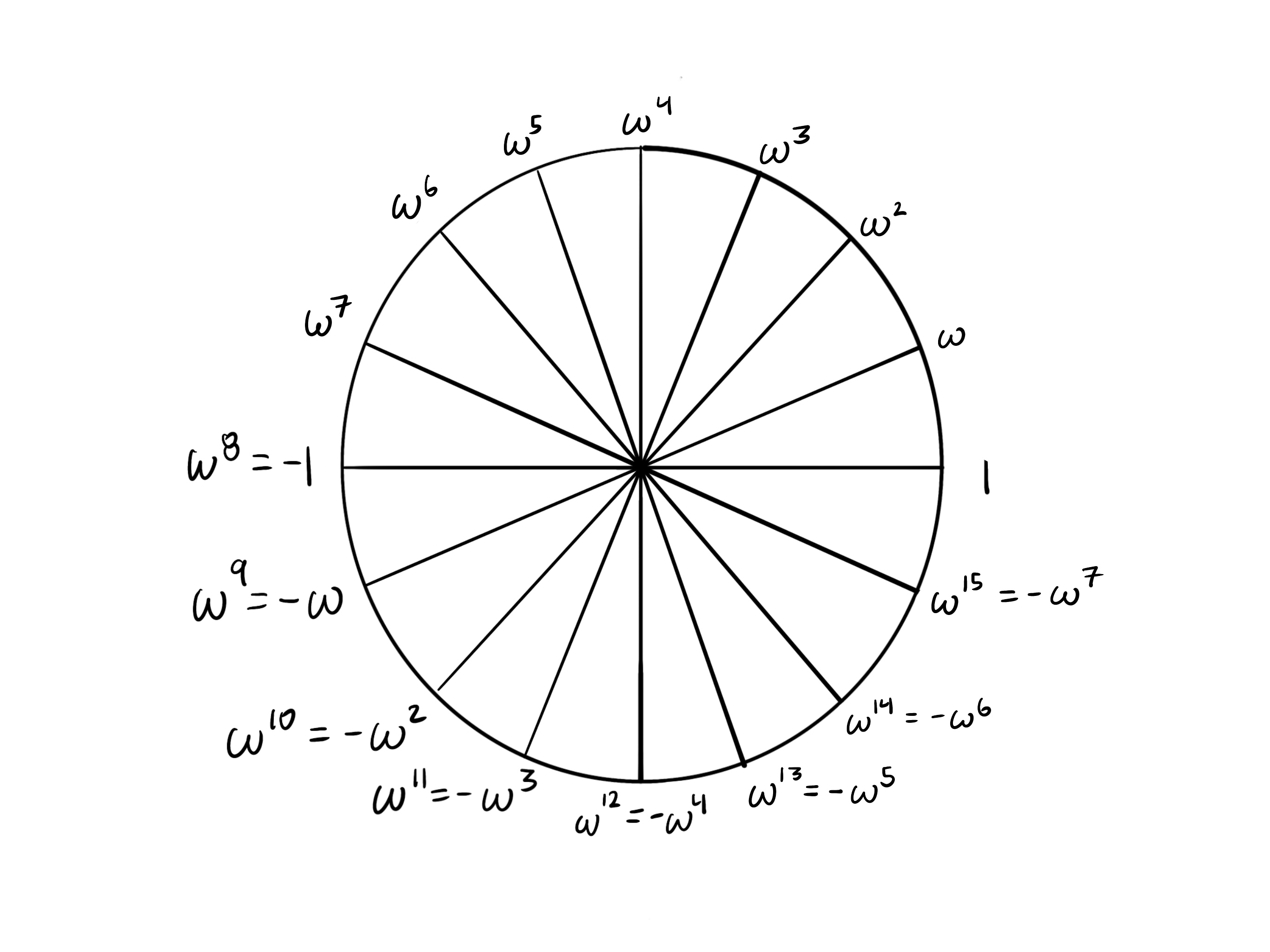
If the circle is partitioned into segments, then taking steps takes you to the opposite side. In each of the cases shown here, we see that opposite points are additive inverses.
k = 8
k = 6
k = 16
Summary
To remember that are additive inverses (their sum is zero), we draw a circle with points where each step is a multiplication by The opposite points will be additive inverses.
The circle diagram will also be very useful for visualizing subgroups of the roots of unity as well as square roots — we will show those visualizations in the upcoming chapters.
Ready to Get Started?
Join Thousands of Users Today
Start your free trial now and experience the difference. No credit card required.