The square of a k-th root of unity is a k/2-th root of unity

If we take the set of $k$-th roots of unity (with $k$ even) and square each element, the resulting set will be a set of half the size. The new set will be the $\frac{k}{2}$-th roots of unity.

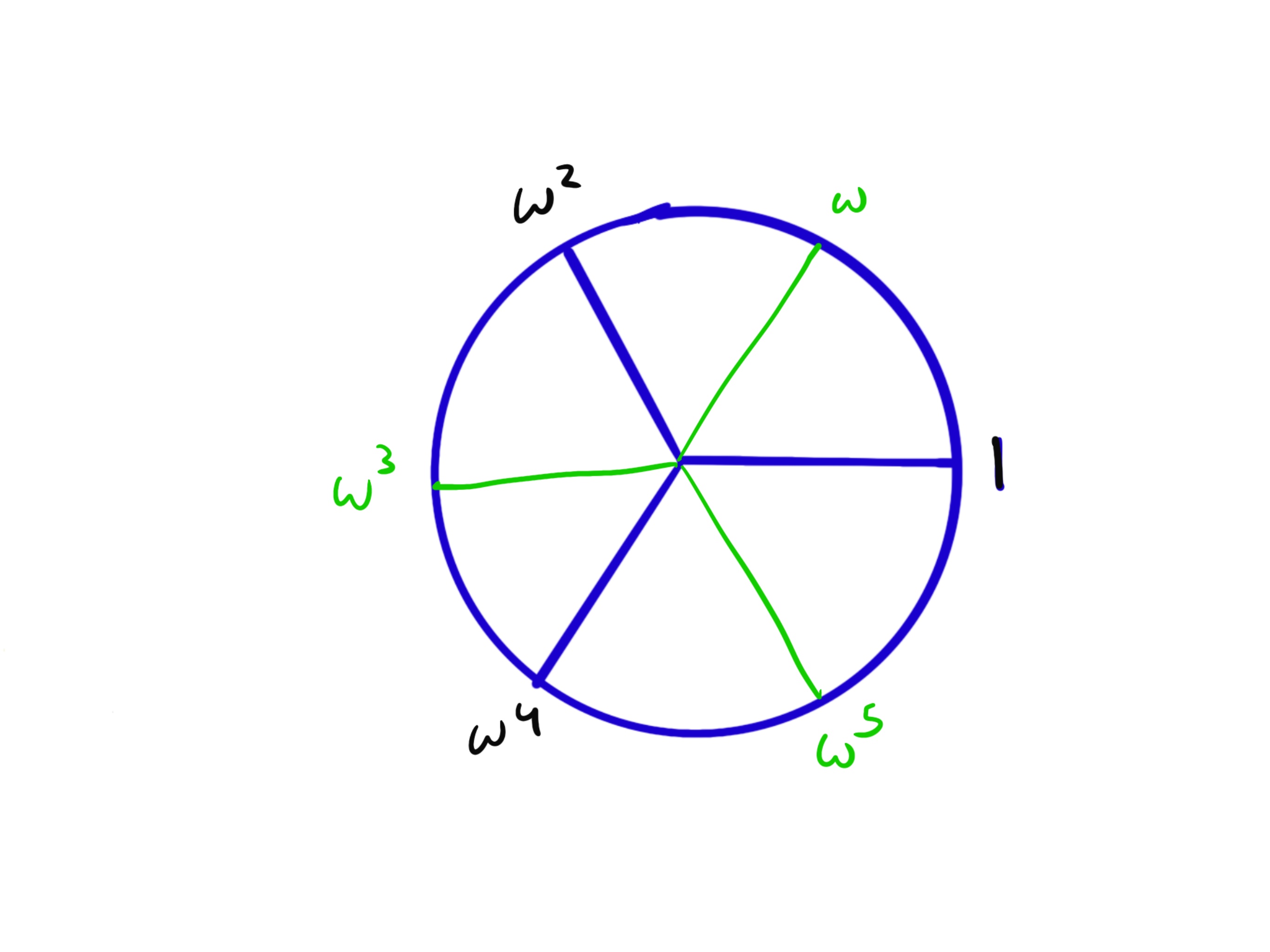
For example, suppose $k = 6$. The 6th roots of unity would be

If we square each element, we get the following set. Some elements have exponents greater than or equal to $k$, but we will handle that in the next step.

We can then factor the exponents as follows:

Since $\omega$ is a 6-th root of unity, $\omega^6\equiv1$ so we have:

Removing multiplication by $1$, we get

Now replace all the duplicate terms with a single element:

The new set is half the size of the original, and each element is a 3-rd root of unity:

• $1^3\equiv1$
• $(\omega^2)^3=\omega^6\equiv1$
• $(\omega^4)^3=\omega^{12}=\omega^6\omega^6\equiv1\cdot1=1$

If we plot the 6-th roots of unity on a circle, we can see that squaring “removes” every other element. We started with $\set{1,\omega,\omega^2,\omega^3,\omega^4,\omega^5}$ and ended with $\set{1,\omega^2,\omega^4}$

To reiterate, if we take the set of $k$-th roots of unity, and $k$ is even, then square each element, we get a set of half the size with each element being the $\frac{k}{2}$-th root of unity.

Some more examples:

• If $k = 10$ and we square each of the 10-th roots of unity, we get a set of size five which are the fifth roots of unity.
• If $k = 8$ and we square each of the 8-th roots of unity, we get a set of size four which is the fourth roots of unity.
• If $k = 4$ and we square each of the 4-th roots of unity, we get a set of size two which is the 2-nd roots of unity.
• If $k = 2$ and we square each of the 2-nd roots of unity, we get a set of size 1 which is just the element 1.

The last point is easily illustrated. The second roots of unity are square roots of 1, which are always $\set{1,-1}\equiv\set{1,\omega^{k/2}}$. Squaring 1 results in 1 and squaring -1 results in 1. Equivalently, $(\omega^{k/2})^2=\omega^k\equiv1$.

Example of squaring the 8-th roots of unity

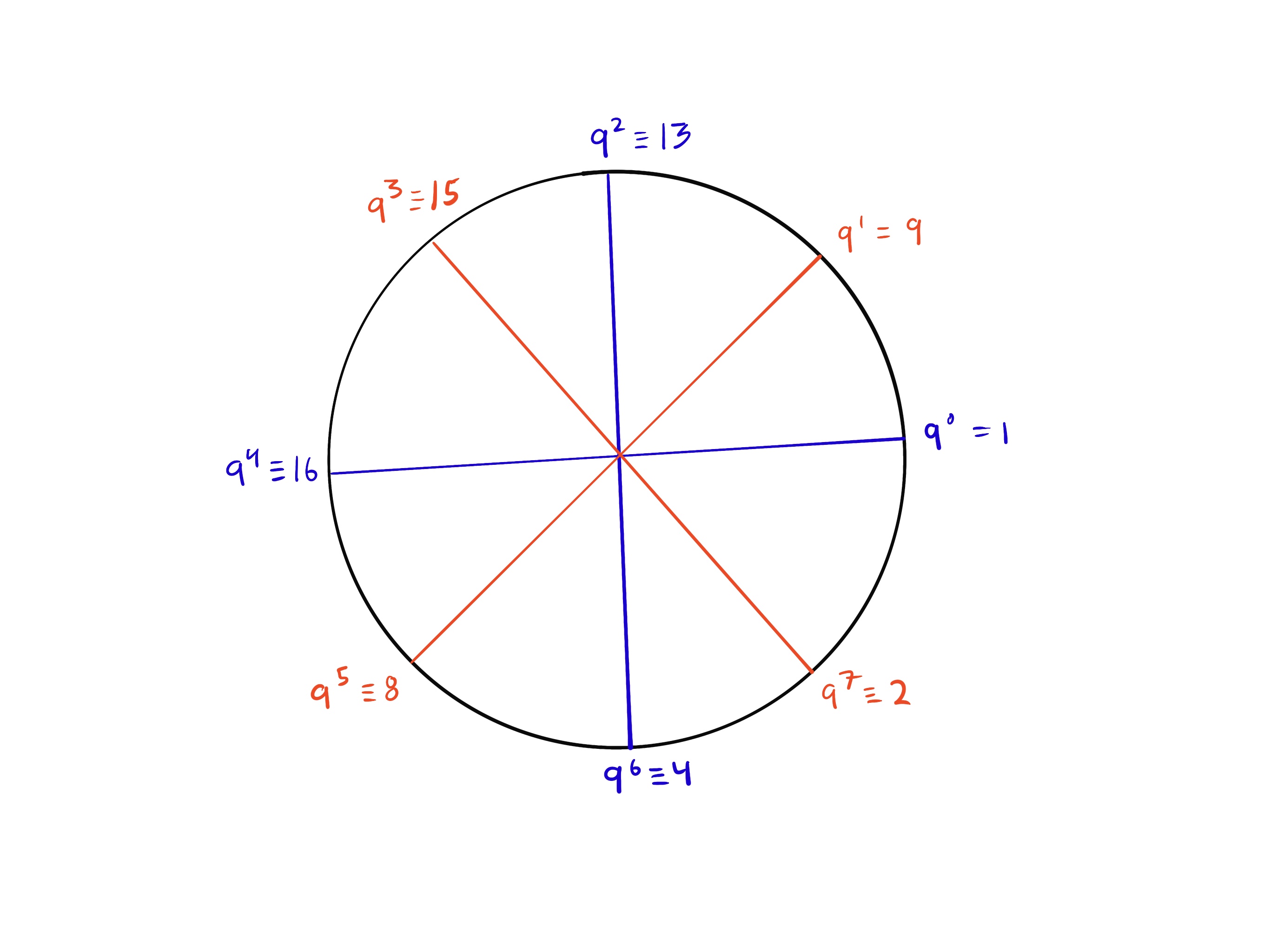
Consider the subgroup of 8th roots of unity $\langle 9\rangle = \{1, 9, 13, 15, 16, 8, 4, 2\}$ in the finite field $\mathbb{F}_{17}$. We square all elements of this subgroup as follows:

The set obtained after squaring is $\{1,13,16,4\}$, which is precisely the subgroup of 4th roots of unity.

Here is a visualization of the roots of unity before and after squaring. We started with the set $\set{1, 9, 13, 15, 16, 8, 4, 2}$ and ended with the set $\set{1,13,16,4}$

k must be even

If $k$ is odd, then there is no such thing as “half of the group” as an odd-sized set cannot be divided into two. For the purposes of NTT, we only deal with even-sized $k$, so we aren’t interested in the case where $k$ is odd.

Proof of the claim that the new set is half the size

Let $\omega$ be a primitive $k$-th root of unity with $k$ even. Let $\langle\omega\rangle$ be the subgroup generated by $\omega$ of order $k$. We claim that $|\set{\omega^2|\omega\in\langle\omega\rangle}|=k/2$.

The proof is actually quite simple and intuitive.

We established in an earlier chapter that $\omega^{i}$ and $\omega^{i+k/2}$ are additive inverses. Since $k$ is even, we can partition the group into two sets, the first one being $0...(k/2-1)$ and the second being $k/2...k-1$:

Those elements are congruent to the following representation:

If we apply $f(x)=x^2$ to both sets, we get two sets with identical content and size $k/2$

Since the two sets are identical, the union of the two sets will be the same size, which is $k/2$.

Proof that squaring a $k$-th root of unity produces a $k/2$-th root of unity

Suppose $a$ is a $k$-th root of unity. We aim to show that $a^2$ is a $\frac{k}{2}$-th root of unity, that is:

Let’s simplify $(a^2)^{\frac{k}{2}}$:

Since $a^k\equiv1$ (because $a$ is a $k$-th root of unity), it follows that $(a^2)^{\frac{k}{2}}\equiv 1$.

Therefore, $a^2$ is indeed a $\frac{k}{2}$-th root of unity.