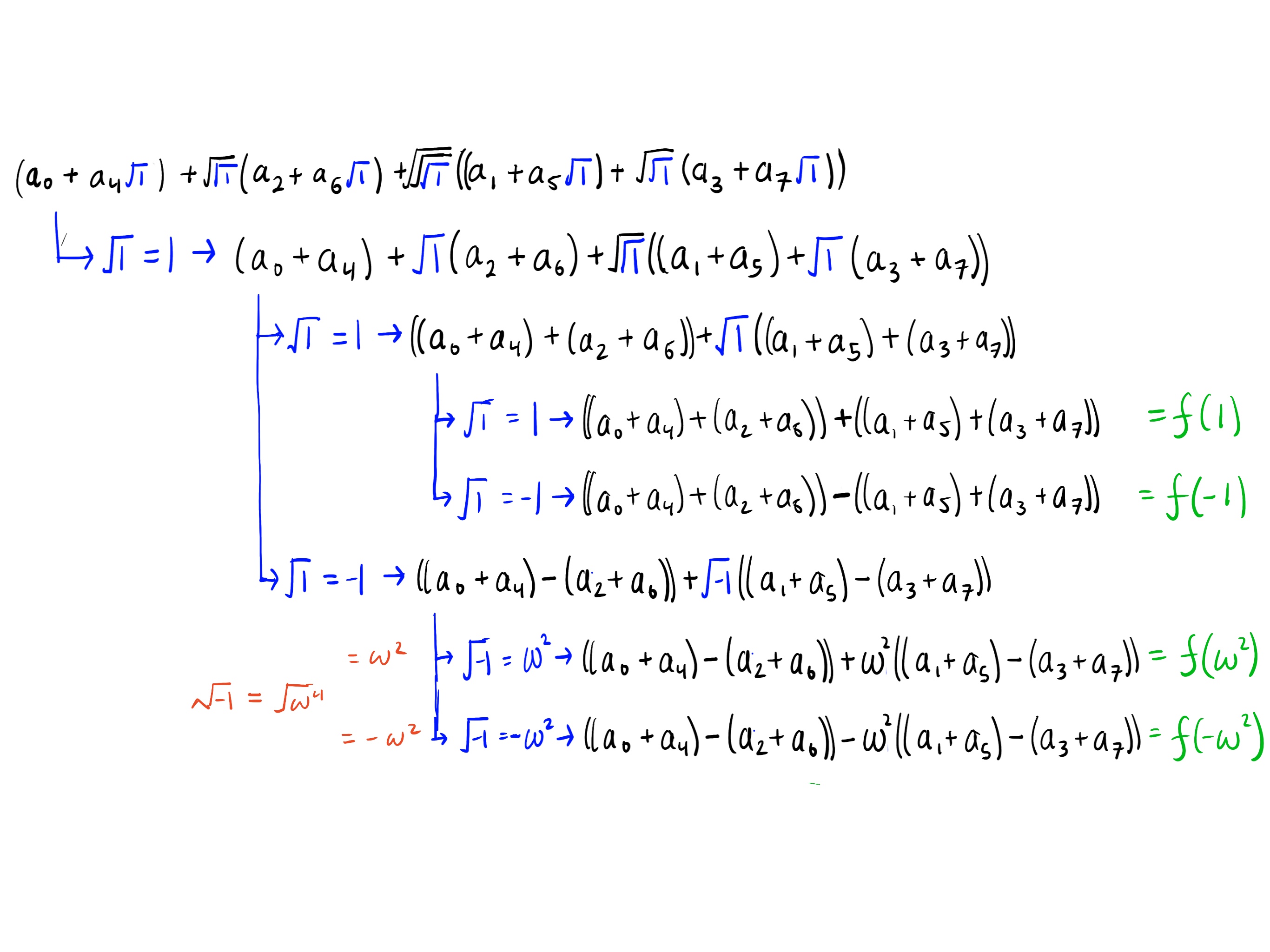NTT Algorithm By Hand
The NTT (Number Theoretic Transform) algorithm converts a polynomial in a finite field from coefficient form to point form.
If a polynomial has degree d d d k k k k > d . k\gt d. k > d .
Rather than evaluating the polynomial f ( x ) f(x) f ( x ) k k k { 1 , ω , ω 2 , . . . , ω k − 1 } \set{1,\omega,\omega^2,...,\omega^{k-1}} { 1 , ω , ω 2 , ... , ω k − 1 } image preservation theorem for multivalued functions to evaluate the multivalued function created by substituting x x x f f f x k \sqrt[k]{x} k x { 1 } \set{1} { 1 } { 1 } \set{1} { 1 } { 1 , ω k / 2 } \set{1,\omega^{k/2}} { 1 , ω k /2 } { 1 , ω k / 4 , ω k / 2 , − ω k / 4 } \set{1,\omega^{k/4},\omega^{k/2},-\omega^{k/4}} { 1 , ω k /4 , ω k /2 , − ω k /4 } k k k
The runtime of this method is O ( n log n ) \mathcal{O}(n \log n) O ( n log n )
Evaluating f ( x ) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 f(x)=a_0+a_1x+a_2x^2+a_3x^3 f ( x ) = a 0 + a 1 x + a 2 x 2 + a 3 x 3
First, we factor the function to maximize the occurrences of x 2 x^2 x 2 2 = k / 2 2=k/2 2 = k /2 x k / 2 x^{k/2} x k /2 { 1 , − 1 } \set{1,-1} { 1 , − 1 }
This creates the following function:
f ( x ) = a 0 + a 2 x 2 + x ( a 1 + a 3 x 2 ) f(x)=a_0+a_2x^2+x(a_1+a_3x^2) f ( x ) = a 0 + a 2 x 2 + x ( a 1 + a 3 x 2 )
Next, we transform f f f x → x 4 x\rightarrow\sqrt[4]{x} x → 4 x
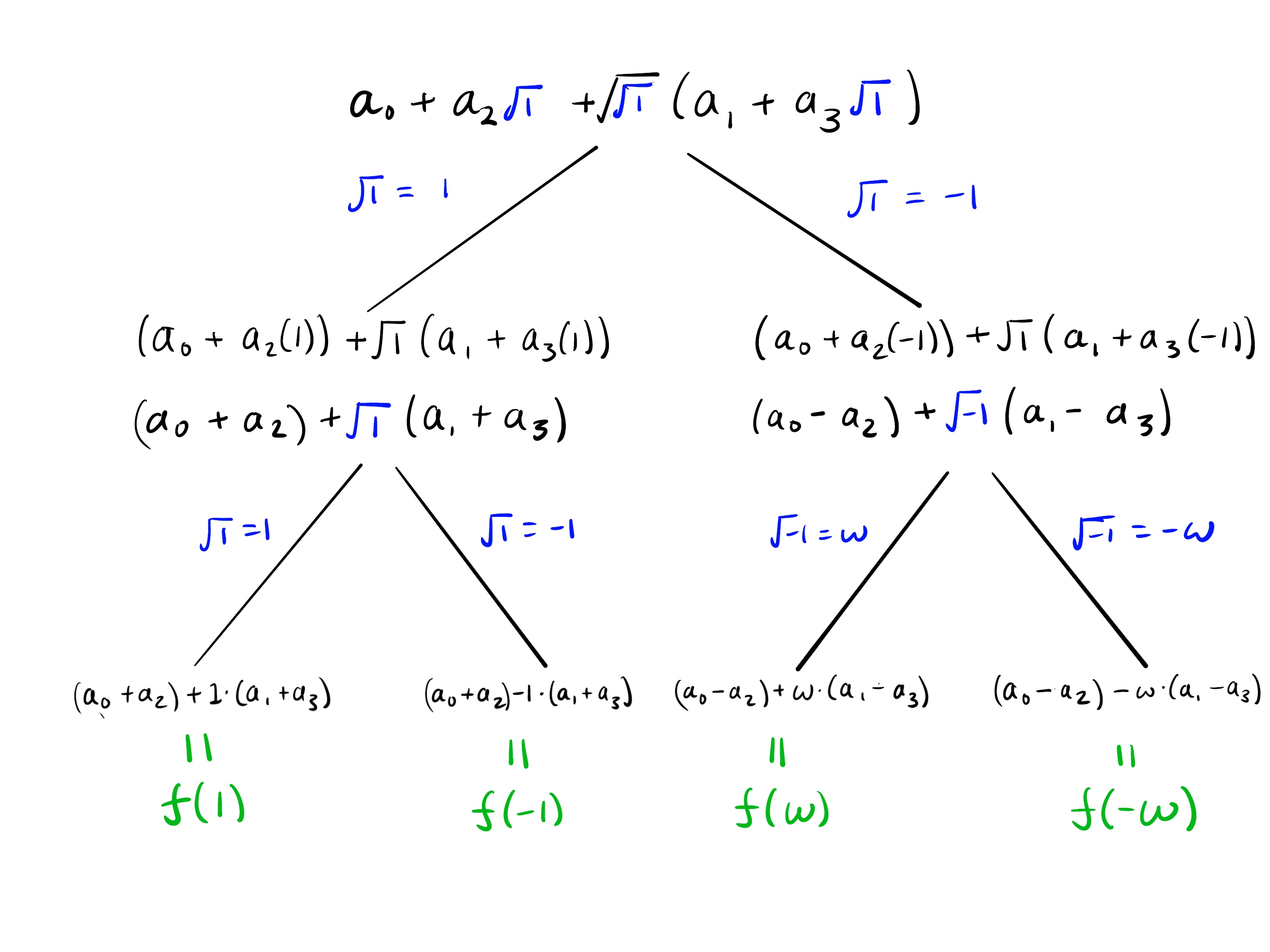
f ( x ) = a 0 + a 2 x + x 4 ( a 1 + a 3 x ) f(x)=a_0+a_2\sqrt{x}+\sqrt[4]{x}(a_1+a_3\sqrt{x}) f ( x ) = a 0 + a 2 x + 4 x ( a 1 + a 3 x )
Here is the square root expansion diagram:
Now we compare the result to evaluating f ( x ) f(x) f ( x )
f ( 1 ) = a 0 + a 1 ( 1 ) + a 2 ( 1 ) 2 + a 3 ( 1 ) 3 f ( − 1 ) = a 0 + a 1 ( − 1 ) + a 2 ( − 1 ) 2 + a 3 ( − 1 ) 3 f ( ω ) = a 0 + a 1 ( ω ) + a 2 ( ω ) 2 + a 3 ( ω ) 3 f ( − ω ) = a 0 + a 1 ( − ω ) + a 2 ( − ω ) 2 + a 3 ( − ω ) 3 \begin{align*}
f(1) &= a_0 &+& a_1(1) &+& a_2(1)^2 &+& a_3(1)^3\\
f(-1) &= a_0 &+& a_1(-1) &+& a_2(-1)^2 &+& a_3(-1)^3\\
f(\omega) &= a_0 &+& a_1(\omega) &+& a_2(\omega)^2 &+& a_3(\omega)^3\\
f(-\omega) &= a_0 &+& a_1(-\omega) &+& a_2(-\omega)^2 &+& a_3(-\omega)^3
\end{align*} f ( 1 ) f ( − 1 ) f ( ω ) f ( − ω ) = a 0 = a 0 = a 0 = a 0 + + + + a 1 ( 1 ) a 1 ( − 1 ) a 1 ( ω ) a 1 ( − ω ) + + + + a 2 ( 1 ) 2 a 2 ( − 1 ) 2 a 2 ( ω ) 2 a 2 ( − ω ) 2 + + + + a 3 ( 1 ) 3 a 3 ( − 1 ) 3 a 3 ( ω ) 3 a 3 ( − ω ) 3
We have that ω 2 = ( − ω 2 ) = − 1 \omega^2=(-\omega^2)=-1 ω 2 = ( − ω 2 ) = − 1 ω 3 = − ω \omega^3=-\omega ω 3 = − ω ( − ω ) 3 = ( − 1 ) 3 ( ω ) 3 = − ω 3 = − ( − ω ) = ω (-\omega)^3=(-1)^3(\omega)^3=-\omega^3=-(-\omega)=\omega ( − ω ) 3 = ( − 1 ) 3 ( ω ) 3 = − ω 3 = − ( − ω ) = ω
f ( 1 ) = a 0 + a 1 + a 2 + a 3 f ( − 1 ) = a 0 − a 1 + a 2 − a 3 f ( ω ) = a 0 + a 1 ω − a 2 − a 3 ω f ( − ω ) = a 0 − a 1 ω − a 2 + a 3 ω \begin{align*}
f(1) &= a_0 &+& a_1 &+& a_2 &+& a_3\\
f(-1) &= a_0 &-& a_1 &+& a_2 &-& a_3\\
f(\omega) &= a_0 &+& a_1\omega &-& a_2 &-& a_3\omega\\
f(-\omega) &= a_0 &-& a_1\omega &-& a_2 &+& a_3\omega
\end{align*} f ( 1 ) f ( − 1 ) f ( ω ) f ( − ω ) = a 0 = a 0 = a 0 = a 0 + − + − a 1 a 1 a 1 ω a 1 ω + + − − a 2 a 2 a 2 a 2 + − − + a 3 a 3 a 3 ω a 3 ω
Exercise: Use the above method to evaluate a 0 + a 1 x + a 2 x 2 a_0+a_1x+a_2x^2 a 0 + a 1 x + a 2 x 2 a 3 = 0 a_3=0 a 3 = 0
The height of the tree is log n \log n log n O ( n ) \mathcal{O}(n) O ( n ) O ( n log n ) \mathcal{O}(n \log n) O ( n log n )
Evaluating f ( x ) = a 0 + a 1 x + . . . + a 7 x 7 f(x)=a_0+a_1x+...+a_7x^7 f ( x ) = a 0 + a 1 x + ... + a 7 x 7
First, we rearrange the polynomial to maximize the number of x 4 x^4 x 4
f ( x ) = a 0 + a 4 x 4 + x 2 ( a 2 + a 6 x 4 ) + x ( ( a 1 + a 5 x 4 ) + x 2 ( a 3 + a 7 x 4 ) ) f(x)=a_0+a_4x^4+x^2(a_2+a_6x^4)+x((a_1+a_5x^4)+x^2(a_3+a_7x^4)) f ( x ) = a 0 + a 4 x 4 + x 2 ( a 2 + a 6 x 4 ) + x (( a 1 + a 5 x 4 ) + x 2 ( a 3 + a 7 x 4 ))
Now we substitute x → x 8 x\rightarrow\sqrt[8]{x} x → 8 x g ( x ) g(x) g ( x )
g ( x ) = a 0 + a 4 x + x 4 ( a 2 + a 6 x ) + x 8 ( ( a 1 + a 5 x ) + x 4 ( a 3 + a 7 x ) ) g(x)=a_0+a_4\sqrt{x}+\sqrt[4]{x}(a_2+a_6\sqrt{x})+\sqrt[8]{x}((a_1+a_5\sqrt{x})+\sqrt[4]{x}(a_3+a_7\sqrt{x})) g ( x ) = a 0 + a 4 x + 4 x ( a 2 + a 6 x ) + 8 x (( a 1 + a 5 x ) + 4 x ( a 3 + a 7 x ))
Since drawing the evaluation tree in one image would be quite large, we’ll draw the left side of the tree where we evaluate 1 = 1 \sqrt{1}=1 1 = 1
From the image above, we have that
f ( 1 ) = ( ( a 0 + a 4 ) + ( a 2 + a 6 ) ) + ( ( a 1 + a 5 ) + ( a 3 + a 7 ) ) f ( − 1 ) = ( ( a 0 + a 4 ) + ( a 2 + a 6 ) ) + ( ( a 1 + a 5 ) + ( a 3 + a 7 ) ) f ( ω 2 ) = ( ( a 0 + a 4 ) − ( a 2 + a 6 ) ) + ω ( ( a 1 + a 5 ) − ( a 3 + a 7 ) ) f ( − ω 2 ) = ( ( a 0 + a 4 ) − ( a 2 + a 6 ) ) − ω ( ( a 1 + a 5 ) − ( a 3 + a 7 ) ) \begin{align*}
f(1)=((a_0+a_4)+(a_2+a_6))+((a_1+a_5)+(a_3+a_7))\\
f(-1)=((a_0+a_4)+(a_2+a_6))+((a_1+a_5)+(a_3+a_7))\\
f(\omega^2)=((a_0+a_4)-(a_2+a_6))+\omega((a_1+a_5)-(a_3+a_7))\\
f(-\omega^2)=((a_0+a_4)-(a_2+a_6))-\omega((a_1+a_5)-(a_3+a_7))\\
\end{align*} f ( 1 ) = (( a 0 + a 4 ) + ( a 2 + a 6 )) + (( a 1 + a 5 ) + ( a 3 + a 7 )) f ( − 1 ) = (( a 0 + a 4 ) + ( a 2 + a 6 )) + (( a 1 + a 5 ) + ( a 3 + a 7 )) f ( ω 2 ) = (( a 0 + a 4 ) − ( a 2 + a 6 )) + ω (( a 1 + a 5 ) − ( a 3 + a 7 )) f ( − ω 2 ) = (( a 0 + a 4 ) − ( a 2 + a 6 )) − ω (( a 1 + a 5 ) − ( a 3 + a 7 ))
Now we expand the right side of the tree where x = − 1 \sqrt{x}=-1 x = − 1
From that result, we have that:
f ( ω ) = ( ( a 0 − a 4 ) + ω 2 ( a 2 − a 6 ) ) + ω ( ( a 1 − a 5 ) + ω 2 ( a 3 − a 7 ) ) f ( − ω ) = ( ( a 0 − a 4 ) + ω 2 ( a 2 − a 6 ) ) − ω ( ( a 1 − a 5 ) + ω 2 ( a 3 − a 7 ) ) f ( ω 3 ) = ( ( a 0 − a 4 ) − ω 2 ( a 2 − a 6 ) ) + ω 3 ( ( a 1 − a 5 ) − ω 2 ( a 3 − a 7 ) ) f ( − ω 3 ) = ( ( a 0 − a 4 ) − ω 2 ( a 2 − a 6 ) ) − ω 3 ( ( a 1 − a 5 ) − ω 2 ( a 3 − a 7 ) ) \begin{align*}
f(\omega)=((a_0-a_4)+\omega^2(a_2-a_6))+\omega((a_1-a_5)+\omega^2(a_3-a_7))\\
f(-\omega)=((a_0-a_4)+\omega^2(a_2-a_6))-\omega((a_1-a_5)+\omega^2(a_3-a_7))\\
f(\omega^3)=((a_0-a_4)-\omega^2(a_2-a_6))+\omega^3((a_1-a_5)-\omega^2(a_3-a_7))\\
f(-\omega^3)=((a_0-a_4)-\omega^2(a_2-a_6))-\omega^3((a_1-a_5)-\omega^2(a_3-a_7))
\end{align*} f ( ω ) = (( a 0 − a 4 ) + ω 2 ( a 2 − a 6 )) + ω (( a 1 − a 5 ) + ω 2 ( a 3 − a 7 )) f ( − ω ) = (( a 0 − a 4 ) + ω 2 ( a 2 − a 6 )) − ω (( a 1 − a 5 ) + ω 2 ( a 3 − a 7 )) f ( ω 3 ) = (( a 0 − a 4 ) − ω 2 ( a 2 − a 6 )) + ω 3 (( a 1 − a 5 ) − ω 2 ( a 3 − a 7 )) f ( − ω 3 ) = (( a 0 − a 4 ) − ω 2 ( a 2 − a 6 )) − ω 3 (( a 1 − a 5 ) − ω 2 ( a 3 − a 7 ))
Combining the evaluations and distributing the omega terms, we have:
f ( 1 ) = a 0 + a 4 + a 2 + a 6 + a 1 + a 5 + a 3 + a 7 f ( − 1 ) = a 0 + a 4 + a 2 + a 6 − a 1 − a 5 − a 3 − a 7 f ( ω 2 ) = a 0 + a 4 − a 2 − a 6 + a 1 ω 2 + a 5 ω 2 − a 3 ω 2 − a 7 ω 2 f ( − ω 2 ) = a 0 + a 4 − a 2 − a 6 − a 1 ω 2 − a 5 ω 2 + a 3 ω 2 + a 7 ω 2 f ( ω ) = a 0 − a 4 + a 2 ω 2 − a 6 ω 2 + a 1 ω − a 5 ω + a 3 ω 3 − a 7 ω 3 f ( − ω ) = a 0 − a 4 + a 2 ω 2 − a 6 ω 2 − a 1 ω + a 5 ω − a 3 ω 3 + a 7 ω 3 f ( ω 3 ) = a 0 − a 4 − a 2 ω 2 + a 6 ω 2 + a 1 ω 3 − a 5 ω 3 + a 3 ω − a 7 ω f ( − ω 3 ) = a 0 − a 4 − a 2 ω 2 + a 6 ω 2 − a 1 ω 3 + a 5 ω 3 − a 3 ω a 7 ω \begin{align*}
f(1) &= a_0 &+ a_4 &+ a_2 &+ a_6 &+ a_1 &+ a_5 &+ a_3 &+ a_7\\f(-1) &= a_0 &+ a_4 &+ a_2 &+ a_6 &- a_1 &- a_5 &- a_3 &- a_7\\f(\omega^2) &= a_0 &+ a_4 &- a_2 &- a_6 &+ a_1\omega^2 &+ a_5\omega^2 &- a_3\omega^2 &- a_7\omega^2\\f(-\omega^2)&= a_0 &+ a_4 &- a_2 &- a_6 &- a_1\omega^2 &- a_5\omega^2 &+ a_3\omega^2 &+ a_7\omega^2\\f(\omega) &= a_0 &- a_4 &+ a_2\omega^2 &- a_6\omega^2 &+ a_1\omega &- a_5\omega &+ a_3\omega^3 &- a_7\omega^3\\f(-\omega) &= a_0 &- a_4 &+ a_2\omega^2 &- a_6\omega^2 &- a_1\omega &+ a_5\omega &- a_3\omega^3 &+ a_7\omega^3\\f(\omega^3) &= a_0 &- a_4 &- a_2\omega^2 &+ a_6\omega^2 &+ a_1\omega^3 &- a_5\omega^3 &+ a_3\omega &- a_7\omega\\f(-\omega^3)&= a_0 &- a_4 &- a_2\omega^2 &+ a_6\omega^2 &- a_1\omega^3 &+ a_5\omega^3 &- a_3\omega & a_7\omega\end{align*} f ( 1 ) f ( − 1 ) f ( ω 2 ) f ( − ω 2 ) f ( ω ) f ( − ω ) f ( ω 3 ) f ( − ω 3 ) = a 0 = a 0 = a 0 = a 0 = a 0 = a 0 = a 0 = a 0 + a 4 + a 4 + a 4 + a 4 − a 4 − a 4 − a 4 − a 4 + a 2 + a 2 − a 2 − a 2 + a 2 ω 2 + a 2 ω 2 − a 2 ω 2 − a 2 ω 2 + a 6 + a 6 − a 6 − a 6 − a 6 ω 2 − a 6 ω 2 + a 6 ω 2 + a 6 ω 2 + a 1 − a 1 + a 1 ω 2 − a 1 ω 2 + a 1 ω − a 1 ω + a 1 ω 3 − a 1 ω 3 + a 5 − a 5 + a 5 ω 2 − a 5 ω 2 − a 5 ω + a 5 ω − a 5 ω 3 + a 5 ω 3 + a 3 − a 3 − a 3 ω 2 + a 3 ω 2 + a 3 ω 3 − a 3 ω 3 + a 3 ω − a 3 ω + a 7 − a 7 − a 7 ω 2 + a 7 ω 2 − a 7 ω 3 + a 7 ω 3 − a 7 ω a 7 ω
Next, we put the coefficients in ascending order:
f ( 1 ) = a 0 + a 1 + a 2 + a 3 + a 4 + a 5 + a 6 + a 7 f ( − 1 ) = a 0 − a 1 + a 2 − a 3 + a 4 − a 5 + a 6 − a 7 f ( ω 2 ) = a 0 + a 1 ω 2 − a 2 − a 3 ω 2 + a 4 + a 5 ω 2 − a 6 − a 7 ω 2 f ( − ω 2 ) = a 0 − a 1 ω 2 − a 2 + a 3 ω 2 + a 4 − a 5 ω 2 − a 6 + a 7 ω 2 f ( ω ) = a 0 + a 1 ω + a 2 ω 2 + a 3 ω 3 − a 4 − a 5 ω − a 6 ω 2 − a 7 ω 3 f ( − ω ) = a 0 − a 1 ω + a 2 ω 2 − a 3 ω 3 − a 4 + a 5 ω − a 6 ω 2 + a 7 ω 3 f ( ω 3 ) = a 0 + a 1 ω 3 − a 2 ω 2 + a 3 ω − a 4 − a 5 ω 3 + a 6 ω 2 − a 7 ω f ( − ω 3 ) = a 0 − a 1 ω 3 − a 2 ω 2 − a 3 ω − a 4 + a 5 ω 3 + a 6 ω 2 + a 7 ω \begin{align*}
f(1) &= a_0 &+ a_1 &+ a_2 &+ a_3 &+ a_4 &+ a_5 &+ a_6 &+ a_7\\
f(-1) &= a_0 &- a_1 &+ a_2 &- a_3 &+ a_4 &- a_5 &+ a_6 &- a_7\\
f(\omega^2) &= a_0 &+ a_1\omega^2 &- a_2 &- a_3\omega^2 &+ a_4 &+ a_5\omega^2 &- a_6 &- a_7\omega^2\\
f(-\omega^2)&= a_0 &- a_1\omega^2 &- a_2 &+ a_3\omega^2 &+ a_4 &- a_5\omega^2 &- a_6 &+ a_7\omega^2\\
f(\omega) &= a_0 &+ a_1\omega &+ a_2\omega^2 &+ a_3\omega^3 &- a_4 &- a_5\omega &- a_6\omega^2 &- a_7\omega^3\\
f(-\omega) &= a_0 &- a_1\omega &+ a_2\omega^2 &- a_3\omega^3 &- a_4 &+ a_5\omega &- a_6\omega^2 &+ a_7\omega^3\\
f(\omega^3) &= a_0 &+ a_1\omega^3 &- a_2\omega^2 &+ a_3\omega &- a_4 &- a_5\omega^3 &+ a_6\omega^2 &- a_7\omega\\
f(-\omega^3)&= a_0 &- a_1\omega^3 &- a_2\omega^2 &- a_3\omega &- a_4 &+ a_5\omega^3 &+ a_6\omega^2 &+ a_7\omega
\end{align*} f ( 1 ) f ( − 1 ) f ( ω 2 ) f ( − ω 2 ) f ( ω ) f ( − ω ) f ( ω 3 ) f ( − ω 3 ) = a 0 = a 0 = a 0 = a 0 = a 0 = a 0 = a 0 = a 0 + a 1 − a 1 + a 1 ω 2 − a 1 ω 2 + a 1 ω − a 1 ω + a 1 ω 3 − a 1 ω 3 + a 2 + a 2 − a 2 − a 2 + a 2 ω 2 + a 2 ω 2 − a 2 ω 2 − a 2 ω 2 + a 3 − a 3 − a 3 ω 2 + a 3 ω 2 + a 3 ω 3 − a 3 ω 3 + a 3 ω − a 3 ω + a 4 + a 4 + a 4 + a 4 − a 4 − a 4 − a 4 − a 4 + a 5 − a 5 + a 5 ω 2 − a 5 ω 2 − a 5 ω + a 5 ω − a 5 ω 3 + a 5 ω 3 + a 6 + a 6 − a 6 − a 6 − a 6 ω 2 − a 6 ω 2 + a 6 ω 2 + a 6 ω 2 + a 7 − a 7 − a 7 ω 2 + a 7 ω 2 − a 7 ω 3 + a 7 ω 3 − a 7 ω + a 7 ω
Now let’s rearrange the evaluations to go from f ( 1 ) f(1) f ( 1 ) f ( ω ) f(\omega) f ( ω ) f ( ω 7 ) f(\omega^7) f ( ω 7 )
f ( 1 ) = a 0 + a 1 + a 2 + a 3 + a 4 + a 5 + a 6 + a 7 f ( ω ) = a 0 + a 1 ω + a 2 ω 2 + a 3 ω 3 − a 4 − a 5 ω − a 6 ω 2 − a 7 ω 3 f ( ω 2 ) = a 0 + a 1 ω 2 − a 2 − a 3 ω 2 + a 4 + a 5 ω 2 − a 6 − a 7 ω 2 f ( ω 3 ) = a 0 + a 1 ω 3 − a 2 ω 2 + a 3 ω − a 4 − a 5 ω 3 + a 6 ω 2 − a 7 ω f ( − 1 ) = a 0 − a 1 + a 2 − a 3 + a 4 − a 5 + a 6 − a 7 f ( − ω ) = a 0 − a 1 ω + a 2 ω 2 − a 3 ω 3 − a 4 + a 5 ω − a 6 ω 2 + a 7 ω 3 f ( − ω 2 ) = a 0 − a 1 ω 2 − a 2 + a 3 ω 2 + a 4 − a 5 ω 2 − a 6 + a 7 ω 2 f ( − ω 3 ) = a 0 − a 1 ω 3 − a 2 ω 2 − a 3 ω − a 4 + a 5 ω 3 + a 6 ω 2 + a 7 ω \begin{align*}
f(1) &= a_0 &+ a_1 &+ a_2 &+ a_3 &+ a_4 &+ a_5 &+ a_6 &+ a_7\\
f(\omega) &= a_0 &+ a_1\omega &+ a_2\omega^2 &+ a_3\omega^3 &- a_4 &- a_5\omega &- a_6\omega^2 &- a_7\omega^3\\
f(\omega^2) &= a_0 &+ a_1\omega^2 &- a_2 &- a_3\omega^2 &+ a_4 &+ a_5\omega^2 &- a_6 &- a_7\omega^2\\
f(\omega^3) &= a_0 &+ a_1\omega^3 &- a_2\omega^2 &+ a_3\omega &- a_4 &- a_5\omega^3 &+ a_6\omega^2 &- a_7\omega\\
f(-1) &= a_0 &- a_1 &+ a_2 &- a_3 &+ a_4 &- a_5 &+ a_6 &- a_7\\
f(-\omega) &= a_0 &- a_1\omega &+ a_2\omega^2 &- a_3\omega^3 &- a_4 &+ a_5\omega &- a_6\omega^2 &+ a_7\omega^3\\
f(-\omega^2)&= a_0 &- a_1\omega^2 &- a_2 &+ a_3\omega^2 &+ a_4 &- a_5\omega^2 &- a_6 &+ a_7\omega^2\\
f(-\omega^3)&= a_0 &- a_1\omega^3 &- a_2\omega^2 &- a_3\omega &- a_4 &+ a_5\omega^3 &+ a_6\omega^2 &+ a_7\omega
\end{align*} f ( 1 ) f ( ω ) f ( ω 2 ) f ( ω 3 ) f ( − 1 ) f ( − ω ) f ( − ω 2 ) f ( − ω 3 ) = a 0 = a 0 = a 0 = a 0 = a 0 = a 0 = a 0 = a 0 + a 1 + a 1 ω + a 1 ω 2 + a 1 ω 3 − a 1 − a 1 ω − a 1 ω 2 − a 1 ω 3 + a 2 + a 2 ω 2 − a 2 − a 2 ω 2 + a 2 + a 2 ω 2 − a 2 − a 2 ω 2 + a 3 + a 3 ω 3 − a 3 ω 2 + a 3 ω − a 3 − a 3 ω 3 + a 3 ω 2 − a 3 ω + a 4 − a 4 + a 4 − a 4 + a 4 − a 4 + a 4 − a 4 + a 5 − a 5 ω + a 5 ω 2 − a 5 ω 3 − a 5 + a 5 ω − a 5 ω 2 + a 5 ω 3 + a 6 − a 6 ω 2 − a 6 + a 6 ω 2 + a 6 − a 6 ω 2 − a 6 + a 6 ω 2 + a 7 − a 7 ω 3 − a 7 ω 2 − a 7 ω − a 7 + a 7 ω 3 + a 7 ω 2 + a 7 ω
If we compare this to the Vandermonde matrix for the 8-th roots of unity, we can see we correctly computed the powers of ω \omega ω
V = [ 1 1 1 1 1 1 1 1 1 ω ω 2 ω 3 − 1 − ω − ω 2 − ω 3 1 ω 2 − 1 − ω 2 1 ω 2 − 1 − ω 2 1 ω 3 − ω 2 ω − 1 − ω 3 ω 2 − ω 1 − 1 1 − 1 1 − 1 1 − 1 1 − ω ω 2 − ω 3 − 1 ω − ω 2 ω 3 1 − ω 2 − 1 ω 2 1 − ω 2 − 1 ω 2 1 − ω 3 − ω 2 − ω − 1 ω 3 ω 2 ω ] \mathbf{V} =\begin{bmatrix}
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
1 & \omega & \omega^{2} & \omega^{3} & -1 & -\omega & -\omega^{2} & -\omega^{3} \\
1 & \omega^{2} & -1 & -\omega^{2} & 1 & \omega^{2} & -1 & -\omega^{2} \\
1 & \omega^{3} & -\omega^{2} & \omega & -1 & -\omega^{3} & \omega^{2} & -\omega \\
1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\
1 & -\omega & \omega^{2} & -\omega^{3} & -1 & \omega & -\omega^{2} & \omega^{3} \\
1 & -\omega^{2} & -1 & \omega^{2} & 1 & -\omega^{2} & -1 & \omega^{2} \\
1 & -\omega^{3} & -\omega^{2} & -\omega & -1 & \omega^{3} & \omega^{2} & \omega
\end{bmatrix} V = 1 1 1 1 1 1 1 1 1 ω ω 2 ω 3 − 1 − ω − ω 2 − ω 3 1 ω 2 − 1 − ω 2 1 ω 2 − 1 − ω 2 1 ω 3 − ω 2 ω − 1 − ω 3 ω 2 − ω 1 − 1 1 − 1 1 − 1 1 − 1 1 − ω ω 2 − ω 3 − 1 ω − ω 2 ω 3 1 − ω 2 − 1 ω 2 1 − ω 2 − 1 ω 2 1 − ω 3 − ω 2 − ω − 1 ω 3 ω 2 ω
Vandermonde matrix computation
The Vandermonde matrix above was derived as follows. Each row is the powers of x x x f ( x ) = a 0 + a 1 x + . . . + a 7 x 7 f(x)=a_0+a_1x+...+a_7x^7 f ( x ) = a 0 + a 1 x + ... + a 7 x 7 x = { 1 , ω , ω 2 , . . . , ω 7 } x=\set{1,\omega,\omega^2,...,\omega^7} x = { 1 , ω , ω 2 , ... , ω 7 }
V = [ 1 1 1 1 1 1 1 1 1 ω ω 2 ω 3 ω 4 ω 5 ω 6 ω 7 1 ω 2 ω 4 ω 6 ω 8 ω 10 ω 12 ω 14 1 ω 3 ω 6 ω 9 ω 12 ω 15 ω 18 ω 21 1 ω 4 ω 8 ω 12 ω 16 ω 20 ω 24 ω 28 1 ω 5 ω 10 ω 15 ω 20 ω 25 ω 30 ω 35 1 ω 6 ω 12 ω 18 ω 24 ω 30 ω 36 ω 42 1 ω 7 ω 14 ω 21 ω 28 ω 35 ω 42 ω 49 ] \mathbf{V}=
\begin{bmatrix}
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\
1 & \omega & \omega^{2} & \omega^{3} & \omega^{4} & \omega^{5} & \omega^{6} & \omega^{7}\\
1 & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{8} & \omega^{10} & \omega^{12} & \omega^{14}\\
1 & \omega^{3} & \omega^{6} & \omega^{9} & \omega^{12} & \omega^{15} & \omega^{18} & \omega^{21}\\
1 & \omega^{4} & \omega^{8} & \omega^{12} & \omega^{16} & \omega^{20} & \omega^{24} & \omega^{28}\\
1 & \omega^{5} & \omega^{10} & \omega^{15} & \omega^{20} & \omega^{25} & \omega^{30} & \omega^{35}\\
1 & \omega^{6} & \omega^{12} & \omega^{18} & \omega^{24} & \omega^{30} & \omega^{36} & \omega^{42}\\
1 & \omega^{7} & \omega^{14} & \omega^{21} & \omega^{28} & \omega^{35} & \omega^{42} & \omega^{49}
\end{bmatrix} V = 1 1 1 1 1 1 1 1 1 ω ω 2 ω 3 ω 4 ω 5 ω 6 ω 7 1 ω 2 ω 4 ω 6 ω 8 ω 10 ω 12 ω 14 1 ω 3 ω 6 ω 9 ω 12 ω 15 ω 18 ω 21 1 ω 4 ω 8 ω 12 ω 16 ω 20 ω 24 ω 28 1 ω 5 ω 10 ω 15 ω 20 ω 25 ω 30 ω 35 1 ω 6 ω 12 ω 18 ω 24 ω 30 ω 36 ω 42 1 ω 7 ω 14 ω 21 ω 28 ω 35 ω 42 ω 49
Next, we factor out multiples of 8:
V = [ 1 1 1 1 1 1 1 1 1 ω ω 2 ω 3 ω 4 ω 5 ω 6 ω 7 1 ω 2 ω 4 ω 6 ω 8 ω 8 ω 2 ω 8 ω 4 ω 8 ω 6 1 ω 3 ω 6 ω 8 ω ω 8 ω 4 ω 8 ω 7 ω 16 ω 2 ω 16 ω 5 1 ω 4 ω 8 ω 8 ω 4 ω 16 ω 16 ω 4 ω 24 ω 24 ω 4 1 ω 5 ω 8 ω 2 ω 8 ω 7 ω 16 ω 4 ω 24 ω ω 24 ω 6 ω 32 ω 3 1 ω 6 ω 8 ω 4 ω 16 ω 2 ω 24 ω 24 ω 6 ω 32 ω 4 ω 40 ω 2 1 ω 7 ω 8 ω 6 ω 16 ω 5 ω 24 ω 4 ω 32 ω 3 ω 40 ω 2 ω 48 ω ] \mathbf{V}=
\begin{bmatrix}
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\
1 & \omega & \omega^{2} & \omega^{3} & \omega^{4} & \omega^{5} & \omega^{6} & \omega^{7}\\
1 & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{8} & \omega^{8}\omega^{2} & \omega^{8}\omega^{4} & \omega^{8}\omega^{6}\\
1 & \omega^{3} & \omega^{6} & \omega^{8}\omega & \omega^{8}\omega^{4} & \omega^{8}\omega^{7} & \omega^{16}\omega^{2} & \omega^{16}\omega^{5}\\
1 & \omega^{4} & \omega^{8} & \omega^{8}\omega^{4} & \omega^{16} & \omega^{16}\omega^{4} & \omega^{24} & \omega^{24}\omega^{4}\\
1 & \omega^{5} & \omega^{8}\omega^{2} & \omega^{8}\omega^{7} & \omega^{16}\omega^{4} & \omega^{24}\omega & \omega^{24}\omega^{6} & \omega^{32}\omega^{3}\\
1 & \omega^{6} & \omega^{8}\omega^{4} & \omega^{16}\omega^{2} & \omega^{24} & \omega^{24}\omega^{6} & \omega^{32}\omega^{4} & \omega^{40}\omega^{2}\\
1 & \omega^{7} & \omega^{8}\omega^{6} & \omega^{16}\omega^{5} & \omega^{24}\omega^{4} & \omega^{32}\omega^{3} & \omega^{40}\omega^{2} & \omega^{48}\omega\\
\end{bmatrix} V = 1 1 1 1 1 1 1 1 1 ω ω 2 ω 3 ω 4 ω 5 ω 6 ω 7 1 ω 2 ω 4 ω 6 ω 8 ω 8 ω 2 ω 8 ω 4 ω 8 ω 6 1 ω 3 ω 6 ω 8 ω ω 8 ω 4 ω 8 ω 7 ω 16 ω 2 ω 16 ω 5 1 ω 4 ω 8 ω 8 ω 4 ω 16 ω 16 ω 4 ω 24 ω 24 ω 4 1 ω 5 ω 8 ω 2 ω 8 ω 7 ω 16 ω 4 ω 24 ω ω 24 ω 6 ω 32 ω 3 1 ω 6 ω 8 ω 4 ω 16 ω 2 ω 24 ω 24 ω 6 ω 32 ω 4 ω 40 ω 2 1 ω 7 ω 8 ω 6 ω 16 ω 5 ω 24 ω 4 ω 32 ω 3 ω 40 ω 2 ω 48 ω
Removing the factors of 8 we have:
V = [ 1 1 1 1 1 1 1 1 1 ω ω 2 ω 3 ω 4 ω 5 ω 6 ω 7 1 ω 2 ω 4 ω 6 1 ω 2 ω 4 ω 6 1 ω 3 ω 6 ω ω 4 ω 7 ω 2 ω 5 1 ω 4 1 ω 4 1 ω 4 1 ω 4 1 ω 5 ω 2 ω 7 ω 4 ω ω 6 ω 3 1 ω 6 ω 4 ω 2 1 ω 6 ω 4 ω 2 1 ω 7 ω 6 ω 5 ω 4 ω 3 ω 2 ω ] \mathbf{V} =
\begin{bmatrix}
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\
1 & \omega & \omega^{2} & \omega^{3} & \omega^{4} & \omega^{5} & \omega^{6} & \omega^{7}\\
1 & \omega^{2} & \omega^{4} & \omega^{6} & 1 & \omega^{2} & \omega^{4} & \omega^{6}\\
1 & \omega^{3} & \omega^{6} & \omega & \omega^{4} & \omega^{7} & \omega^{2} & \omega^{5}\\
1 & \omega^{4} & 1 & \omega^{4} & 1 & \omega^{4} & 1 & \omega^{4}\\
1 & \omega^{5} & \omega^{2} & \omega^{7} & \omega^{4} & \omega & \omega^{6} & \omega^{3}\\
1 & \omega^{6} & \omega^{4} & \omega^{2} & 1 & \omega^{6} & \omega^{4} & \omega^{2}\\
1 & \omega^{7} & \omega^{6} & \omega^{5} & \omega^{4} & \omega^{3} & \omega^{2} & \omega
\end{bmatrix} V = 1 1 1 1 1 1 1 1 1 ω ω 2 ω 3 ω 4 ω 5 ω 6 ω 7 1 ω 2 ω 4 ω 6 1 ω 2 ω 4 ω 6 1 ω 3 ω 6 ω ω 4 ω 7 ω 2 ω 5 1 ω 4 1 ω 4 1 ω 4 1 ω 4 1 ω 5 ω 2 ω 7 ω 4 ω ω 6 ω 3 1 ω 6 ω 4 ω 2 1 ω 6 ω 4 ω 2 1 ω 7 ω 6 ω 5 ω 4 ω 3 ω 2 ω
After replacing ω 4 = − 1 \omega^4=-1 ω 4 = − 1 ω 5 = − ω \omega^5=-\omega ω 5 = − ω ω 6 = − ω 2 \omega^6=-\omega^2 ω 6 = − ω 2 ω 7 = − ω 3 \omega^7=-\omega^3 ω 7 = − ω 3
V = [ 1 1 1 1 1 1 1 1 1 ω ω 2 ω 3 − 1 − ω − ω 2 − ω 3 1 ω 2 − 1 − ω 2 1 ω 2 − 1 − ω 2 1 ω 3 − ω 2 ω − 1 − ω 3 ω 2 − ω 1 − 1 1 − 1 1 − 1 1 − 1 1 − ω ω 2 − ω 3 − 1 ω − ω 2 ω 3 1 − ω 2 − 1 ω 2 1 − ω 2 − 1 ω 2 1 − ω 3 − ω 2 − ω − 1 ω 3 ω 2 ω ] \mathbf{V} =\begin{bmatrix}
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
1 & \omega & \omega^{2} & \omega^{3} & -1 & -\omega & -\omega^{2} & -\omega^{3} \\
1 & \omega^{2} & -1 & -\omega^{2} & 1 & \omega^{2} & -1 & -\omega^{2} \\
1 & \omega^{3} & -\omega^{2} & \omega & -1 & -\omega^{3} & \omega^{2} & -\omega \\
1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\
1 & -\omega & \omega^{2} & -\omega^{3} & -1 & \omega & -\omega^{2} & \omega^{3} \\
1 & -\omega^{2} & -1 & \omega^{2} & 1 & -\omega^{2} & -1 & \omega^{2} \\
1 & -\omega^{3} & -\omega^{2} & -\omega & -1 & \omega^{3} & \omega^{2} & \omega
\end{bmatrix} V = 1 1 1 1 1 1 1 1 1 ω ω 2 ω 3 − 1 − ω − ω 2 − ω 3 1 ω 2 − 1 − ω 2 1 ω 2 − 1 − ω 2 1 ω 3 − ω 2 ω − 1 − ω 3 ω 2 − ω 1 − 1 1 − 1 1 − 1 1 − 1 1 − ω ω 2 − ω 3 − 1 ω − ω 2 ω 3 1 − ω 2 − 1 ω 2 1 − ω 2 − 1 ω 2 1 − ω 3 − ω 2 − ω − 1 ω 3 ω 2 ω
Exercise: Evaluate f ( x ) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4 + a 5 x 5 + a 6 x 6 f(x)=a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5+a_6x^6 f ( x ) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4 + a 5 x 5 + a 6 x 6 a 7 = 0 a_7=0 a 7 = 0
Exercise: Evaluate f ( x ) = 3 + 2 x + 9 x 2 + x 3 f(x)=3 +2x+9x^2+x^3 f ( x ) = 3 + 2 x + 9 x 2 + x 3 F q \mathbb{F}_q F q q = 17 q=17 q = 17
Summary
Evaluating a polynomial on the k k k { 1 } \set{1} { 1 }
This method saves computation cost because at each step, half of the square roots are evaluated and multiplied the coefficient or sum of coefficients they are paired with. For the remaining evaluations, the results are simply copied down instead of being reevaluated.