The Image Preservation Theorem for Multivalued Functions

We’ll start this chapter on an unusual note — the NTT algorithm is quite simple and can be implemented in less than 20 lines of code. However, the key idea that makes it work, oddly enough, does not have a formal mathematical name. So we are going to take the liberty to give what we believe to be the core theorem behind the algorithm a (subjectively) catchy name:

The Image Preservation Theorem for Multivalued Functions

To explain the Image Preservation Theorem, we’ll go over one last (very simple) concept about roots of unity, then introduce the theorem.

$k$-th roots of nested square roots

The literal definition for “k-th root of unity” is that the root of unity $a$ satisfies $a^k\equiv1$. Stated another way:

Therefore, it should be no surprise that if $\omega$ is the primitive 4-th root of unity then

Now let’s do the same operation if $\omega$ is the primitive 8-th root of unity. The result would be

and the 8-th root of 1 generates all the 8-th roots of unity:

These observations are simply a matter of definition. Of course, we do not want to directly compute the square root of 1. It’s much easier to first find the primitive $k$-th root of unity first, then generate the set of answers for $\sqrt[8]{1}$. For example:

import galois
Fq = 17
k = 8
assert (Fq - 1) % k == 0, "no such subgroup"

GF = galois.GF(Fq)

pr = GF.primitive_root_of_unity(k)

roots = []
for i in range(0,k):
    roots.append(pr**i)
print(roots)

We can also observe that:

and so on. As noted above, directly computing the $\sqrt[k]{1}$ is not efficient. Instead, we consider the following diagram, where each arrow down is a square root of the number above it:

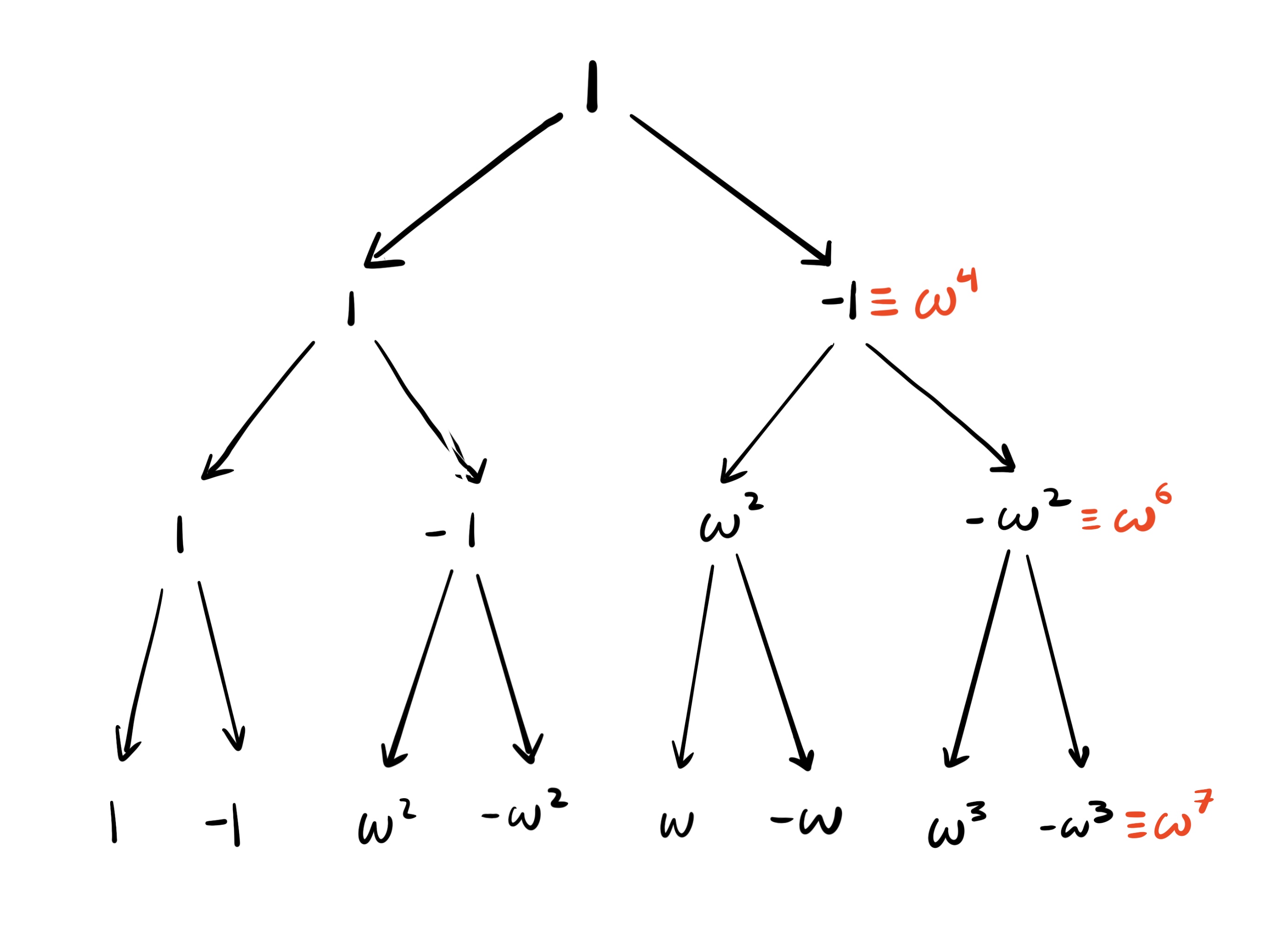
We can compute the 8-th roots of unity by starting with 1 and repeatedly taking square roots.

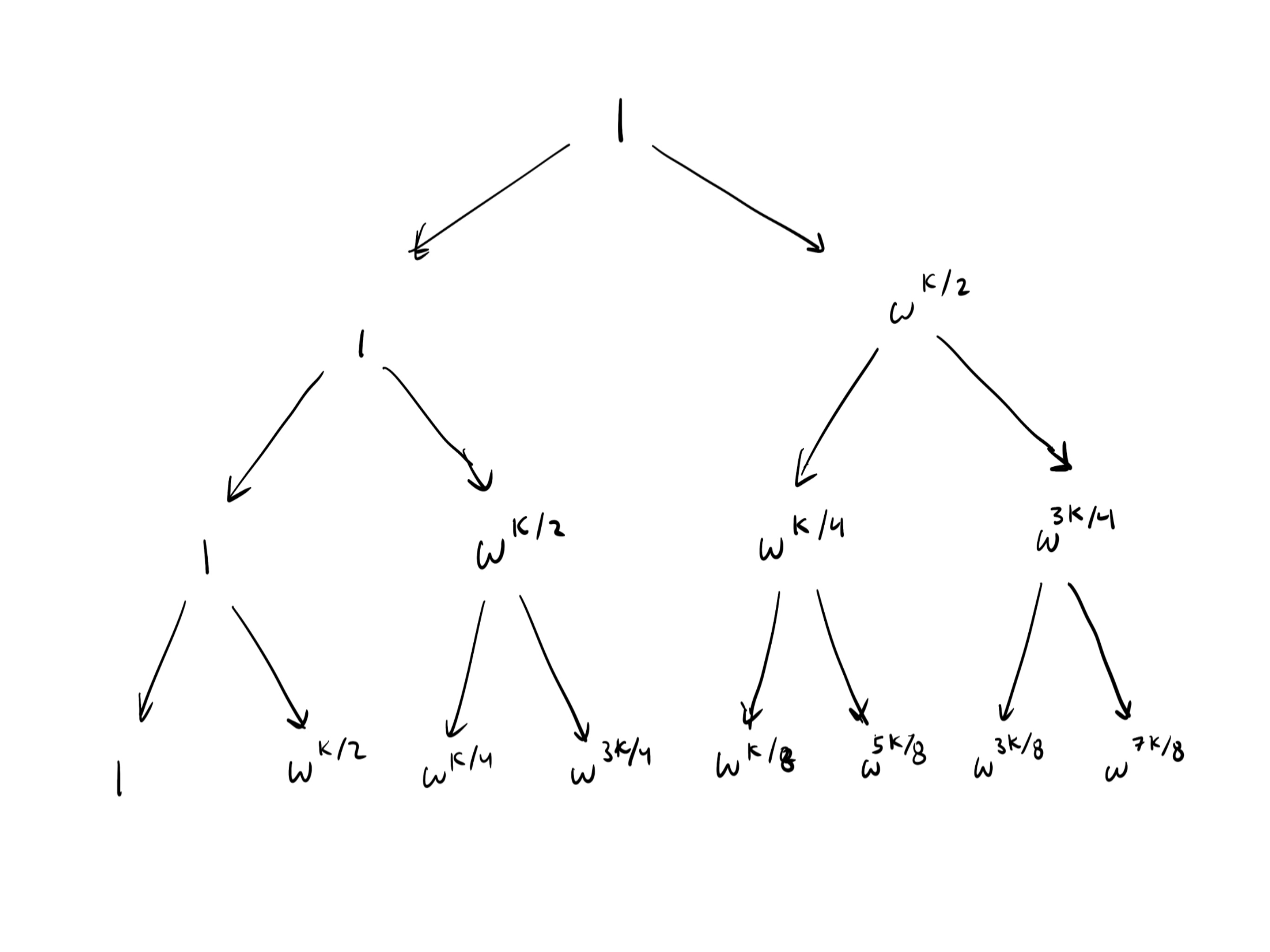
For arbitrary $k$, the diagram is as follows.

Here is a walkthrough of the square root computations:

The square root of 1 is $\set{1,\omega^{k/2}}$. $\omega^{k/2}$ is congruent to -1

Recall from the previous chapter that the square root of $\omega^m$ is $\omega^{m/2}$ and $-\omega^{m/2}$ (assuming $m$ is even).

Thus, the square root of $\omega^{k/2}$ is $\set{\omega^{k/4},-\omega^{k/4}}$.

Also recall that the additive inverse of $\omega^i$ is $\omega^{i+k/2}$.

So to compute $-\omega^{k/4}$ without the negative sign, we compute $\omega^{k/4+k/2}=\omega^{k/4+2k/4}=\omega^{3k/4}$. So the square root of $\omega^{k/2}$ is $\set{\omega^{k/4},\omega^{3k/4}}$.

The square root of $\omega^{k/4}$ is ${\omega^{k/8},-\omega^{k/8}}$. Again, to get rid of the negative sign, we compute $\omega^{k/8+k/2}=\omega^{5k/8}$

Why the square root of $\omega^{3k/4}=\set{\omega^{3k/8},\omega^{7k/8}}$ is left as an exercise for the reader.

The height of the tree is $\log_2n$

Computing the $k$-th roots of unity by repeatedly taking the square roots of 1 creates a “tree” that is $\log_2(n)$ in height.

Conceptualizing intermediate states of the tree

The set

is mathematically equivalent to the 8-th roots of unity. The set is also equivalent:

Which is also equivalent to:

In other words:

Quick aside — multivalued functions and images

Admittedly, the observations we made above are trivial extensions of the definition of $k$-th roots. The more interesting implications of these observations will be shown in the following section. However, it will be helpful to introduce some mathematical terminology first:

Image of a function — if we have a set of points that we evaluate a function on, then the set of evaluations is the image. For example, if the function is $f(x)=2x$ and the domain we evaluate $f$ on is $\set{1,2}$ then the image will be $\set{2,4}$. The term range of a function means the set of values a function could output. In our context, the image of the function refers to the actual set of outputs for a given set of inputs.

Multivalued function — a function that may return more than one evaluation for a single point in the domain. For example, $\sqrt{x}$ evaluated on 0 returns 0, but $\sqrt{x}$ evaluated on 1 returns $\set{1, -1}$.

Note: The multivalued function $f(x)=\sqrt{x}$ has an image larger than its domain.

With these definitions in mind, the reader should understand the following statements:

“The image of $f(x)=x+1$ on the domain $\set{0,2}$ is $\set{1,3}$”

“The image of the multivalued function $f(x)=\sqrt{x}$ on the domain $\set{1}$ is $\set{1,-1}$”

Now we get to a more interesting set of observations.

The image of $f(x)=x$ evaluated on $\set{1,...,\omega^7}$ is the same as $g(x)=\sqrt[8]{x}$ evaluated on $\set{1}$ (k = 8)

This claim is a simple rephrasing of the concepts shown above, so we won’t elaborate further. The interesting part is how we can generalize this to other functions.

The nuance here is that $g(x)$ is a multivalued function that returns eight elements.

The image of $f(x)=ax$ evaluated on the 4-th roots of unity is the same as the multivalued function $g(x)=a\sqrt[4]{x}$ evaluated on $\set{1}$ (k = 4)

Remember, $\sqrt[4]{1}=\set{1,\omega,\omega^2,\omega^3}$, so $a\sqrt[4]{1}=\set{a,a\omega,a\omega^2,a\omega^3}$. This is the same image as evaluating $f$ on each root of unity one-by-one. Since $f(x)=ax$

• $f(1)=a$
• $f(\omega)=a\omega$
• $f(\omega^2)=a\omega^2$
• $f(\omega^3)=a\omega^3$

Exercise for the reader: Let $f(x)=ax+c$. What is the image of $f(x)$ on the 4-th roots of unity? What is the image of the multivalued function $g(x)=a\sqrt[4]{x}+b$ on the domain $\set{1}$?

In the following chapters, we will show how to handle more complex cases like $f(x)=x^2+x^3$, but for now, we show how to actually compute multivalued functions for the simple cases we showed here. But first, let’s give a formal definition to the observation we’ve made so far about image equivalence.

The image of $f(x)=x$ evaluated on the 4-th roots of unity is the same as the multivalued function $g(x)=\sqrt{x}$ evaluated on the second roots of unity $\set{1,-1}$ (k = 4)

This example is very similar to the above, except that we don’t “target” the domain $\set{1}$ but rather $\set{1,-1}$.

We have that

• $g(1)=\sqrt{1}=\set{1,-1}$
• $g(-1)=\sqrt{-1}=\set{\omega,-\omega}$

This is the same image as evaluating $f$ on $\set{1,\omega,-1,-\omega}$

In summary, if we “shrink” the domain by a factor of $r$ and replace every $x$ in $f(x)$ with $\sqrt[r]{x}$ to create a new multivalued function $g$, the images of $f$ and $g$ are identical.

We’ll now formally define the concept we’ve been illustrating

The core theorem of NTT: Image Preservation Theorem for Multivalued Functions

Let $\omega$ be the primitive $k$-th root of unity and $\langle\omega\rangle=\set{1,\omega,\omega^2,...}$ be the $k$-th roots of unity defined in $\mathbb{F}_q$.

Let $k$ be a power of 2.

Let $f(x)$ be a polynomial in $\mathbb{F}_q$. Let $r$ be a power of 2 less than or equal to $k$.

Let $g(x)$ be a multivalued function created by replacing every $x$ in $f(x)$ with $\sqrt[r]{x}$.

Let the domain $\langle\omega\rangle^r$ be $\set{\omega^r|\omega\in \langle\omega\rangle}$. Note that if $r=k$ then $\langle\omega\rangle^r=\set{1}$.

The image of $f$ on $\langle\omega\rangle$ exactly equals the image of $g$ on $\langle\omega\rangle^r$.

It is of utmost importance that the reader understand the theorem above, as it is the key concept that the Number Theoretic Transform relies on!

Here are some examples to enforce the concept:

• The image of $f(x)=x$ on the 4-th roots of unity is equal to the image of $g(x)=\sqrt{x}$ on the second roots of unity (as shown in the previous section).
• The image of $f(x) =x$ on 16th roots of unity is equal to image of $g(x)=\sqrt{x}$ on 8th roots of unity
• The image of $f(x) =x$ on k-th roots of unity is equal to image of $g_1(x)=\sqrt{x}$ on k/2-th roots of unity
• The image of $g_1(x)=\sqrt{x}$ on k/2-th roots of unity is equal to image of $g_2(x)=\sqrt[4]{x}$ on k/4-th roots of unity

The following section shows examples where $f(x)$ is slightly more complex.

Image Preservation Theorem Examples for $f(x)=ax+b$

Let $f(x)=ax+b$ and the domain be the 4-th roots of unity $\set{1,\omega,\omega^2,\omega^3}$.

Let $f_1$ be the multivalued function $a\sqrt{x}+b$ and the domain be$\set{1,-1}$ or equivalently $\set{1,-\omega^2}$.

Let $f_2$ be the multivalued function $a\sqrt[4]{x}+b$ and the domain be $\set{1}$

The images of $f$, $f_1$, and $f_2$ are identical: $\set{a+b,a\omega+b,a\omega^2+b,a\omega^3+b}$

Connection to NTT

Remember, the goal of NTT is to evaluate $f(x)$ on the $k$-th roots of unity in $\mathcal{O}(n\log n)$ time. In other words, we want to compute the image of $f$ on the $k$-th roots of unity.

You can probably guess where this is going.

Computing the image of $f(x)$ on the $k$-th roots of unity is equivalent to computing the image of a new function $g(x)$ defined such that for each $x$ in $f$, $x\rightarrow\sqrt[k]{x}$ evaluated on $\set{1}$.

However, this leaves an open question:

Expanding $\sqrt[k]{x}$ into $\set{1,...,\omega^{k-1}}$ doesn’t directly lead to a speedup. Algorithmically, expanding a $\sqrt[k]{1}$ into the $k$-th roots of unity is the same as evaluating $f(x)$ on the $k$ points. How does this alternate way of evaluating $f(x)$ help us?

In the next chapter, we will demonstrate how to evaluate multi-valued functions using square root expansion and explain how this approach can prevent redundant computation.